Recently, the authors investigated the uncertainty associated with grid- cell data in Geographic Information Systems (GIS), through the use of a model which permits a population of distorted (but equally probable) versions of the same map to be generated and analysed. While this model is easily applied to data such as Digital Elevation Models to determine the uncertainty associated with the products derived from them, it was not applicable to vector data. However, the model has now been enhanced to provide for stochastic distortion of vector data through the creation of separate horizontal positional error fields in the x and y directions, which are then overlaid with the vector data to apply coordinate shifts by which new versions of point, line and polygon data are created. By perturbing the data to generate distorted versions of it, the likely uncertainty of vector data in both position and attribute may be assessed in GIS outputs. This paper explains the background to the model and discusses its implementation and potential applications.
From an historical viewpoint, as users became more experienced with GIS during the 1970s and 80s, there gradually arose a critical awareness of the fact that in many cases they did not know how accurate their system outputs were and whether or not they actually satisfied their needs. This predicament has been caused not only by the false sense of security that computer technology sometimes induces, but also by the lack of theoretical models of spatial data error. The situation has now reached the point where, for government agencies which base their regulatory decisions upon spatial information or in cases where they or private companies sell data for commercial return, there is a growing international trend towards litigation by aggrieved parties seeking compensation on the grounds that decisions are wrongly based due to data inaccuracies, or that they have suffered damage through unknowingly purchasing and using data which had insufficient accuracy to meet their requirements. Software developers and vendors may also be affected since the algorithms they encode in their products can have the potential to induce additional error. Thus, the accuracy issue is of serious concern to all sectors of the geographic information industry.
In recent years, most international spatial data transfer standards have adopted mandatory data quality reporting provisions (Moellering, 1991), which will help address the problem by ensuring that data providers truthfully label their products in such a way that users can assess their fitness for use. However, while this approach has merit there is a presumption that the necessary tools for assessing and communicating spatial data error already exist. Unfortunately, this is not the case and a considerable amount of research still remains to be conducted. Goodchild (1993), for instance, suggests there are only half a dozen commonly accepted models of spatial data error, and Hunter and Beard (1992) have identified at least 150 potential error sources of which we have little or no current understanding.
To help deal with this problem, the authors have developed a model of uncertainty for dealing with spatial data, however before discussing it some explanatory remarks are required regarding the use of the term 'uncertainty'. In the context of geographic data, it is argued there is a clear distinction between 'error' and 'uncertainty', since the former implies that some degree of knowledge has been attained about differences (and the reasons for their occurrence) between the results or observations and the truth to which they pertain. On the other hand, 'uncertainty' conveys the fact that it is the lack of such knowledge which is responsible for hesitancy in accepting those same results or observations without caution, and often the term 'error' is used when it would be more appropriate to use 'uncertainty'.
The uncertainty model that has evolved can be defined as a stochastic process capable of generating a population of distorted versions of the same reality (such as a map), with each version being a sample from the same population. The traditional Gaussian model (where the mean of the population estimates the true value and the standard deviation is a measure of variation in the observations) is one attempt at describing error, but it is global in nature and says nothing about the processes by which error may have accumulated.
The model adopted in this research is viewed as an advance on the Gaussian model since it not only has the ability to show local variation in uncertainty, but also has the advantage of being able to display the effects of error propagation resulting from the various algorithms and process models that have been applied � even though we do not possess propagation models per se. This latter point is particularly important to users, since many software vendors do not divulge the algorithms used in their packages for commercial reasons � which prevents formal mathematical error propagation analysis from being undertaken. By studying different versions of the products created by the model, it is possible to see how differences in output are affected by variations in input. The model was first designed by Goodchild et al. (1992), and its use in assessing the uncertainty of products derived from grid cell data has been reported in Hunter and Goodchild (1994) and Hunter et al. (1994). However, a limitation of that initial version of the model was its inability to represent uncertainty in vector data, and this paper describes an enhanced version of the model which is capable of producing distorted versions of point, line and polygon data. The paper is structured such that the concepts underlying the model are first introduced, followed by the issues affecting its implementation and the variety of ways in which it might be applied in practice.
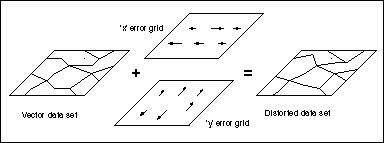
Figure 1. The model of vector uncertainty uses error grids in the x and y directions to produce a distorted version of the data set.
By overlaying the two grids with the data set to be distorted (containing either point, line or polygon features), x and y positional shifts can be applied to the coordinates of each point in the data set to create a new, but equally probable, version of it (Figure 1). Thus, the probabilistic coordinates of a point are considered to be (x + error, y + error). With the distorted version of the data, the user then applies the normal processes required to create the final product, and by using a number of these distorted data sets the uncertainty residing in the end product is able to be assessed. Alternatively, several different data sets may be independently distorted prior to being combined to assess the output uncertainty. While the model does require an initial error estimate for creation of the two grids, it is the resultant uncertainty arising from the use of perturbed data (in conjunction with the spatial operations that are subsequently applied) which is under investigation, and hence its label as an 'uncertainty' model.
Accordingly, the procedure described previously in Hunter and Goodchild (1994) is used to create the grids, which contain a user-defined number of points and a given measure of autocorrelation (rho) in the range 0 < rho < 0.25. The two grids, which are initially assigned zero as their coordinate origin and have unit separation distance between points, are then georeferenced via a 2-dimensional coordinate transformation to achieve the required separation distance and ensure they completely overlap the data set to be perturbed (for example, by using the SHIFT function in Arc Grid which uses the new lower left coordinates of the grid and required point spacing as its arguments).
As a 'rule of thumb' it is suggested that the spacing be equal to or less than 0.5mm at the scale of the map from which the data originated, which is a common estimate of relative positional accuracy. This translates into 0.5m at a scale of 1:1,000, 5m at 1:10,000, and 50m at 1:100,000. Where little is known about the data set's origin, users should select a separation distance smaller than they would care to consider � given the nature of the data and the application concerned. For example, in vegetation boundary data it might be considered that individual boundary segments or polygon widths less than 5m, while not necessarily being spurious, will not practically affect the outcome of the analysis to be conducted. Thus, selection of an error grid separation of 5m is reasonable even though the positional shifts applied to features which are less than this distance apart will be similar in magnitude and therefore highly correlated.
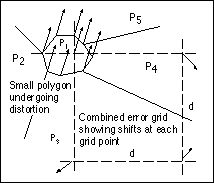
Figure 2. If the spacing (d) between points in the error grids is greater than the smallest feature lengths, then unwanted local correlation between shifts may occur in small features.
To avoid this problem, autocorrelation is introduced during formation of the error grids as mentioned earlier. In this process, the grids are initially populated with random, normally distributed values centered around the nominated mean and standard deviation. For example, if the mean is zero and the standard deviation is 10m, then the properties of the normal distribution are such that approximately 68% of points will be assigned values in the range of 0 �10m, a further 27% will have values between -10m to -20m and +10m to +20m, and the remaining 5% will lie outside of 0 �20m. Then, by an iterative process the values of the original shifts assigned to each grid point are adjusted until the specified level of autocorrelation is achieved, according to the value of the parameter (r) that has been requested.
At this time, it is considered that the rho value required to prevent 'rips' from occurring will depend on the error grid spacing and the standard deviation of the normal distribution being applied, however this has not yet been tested. Instead, a 'trial and error' approach can be adopted whereby rho is increased for each new set of x and y grids until no 'rips' exist, by testing each consecutive pair of points (in horizontal or row sequence for the x grid, and vertical or column sequence for the y grid) to determine whether the absolute value of the difference between their shifts is greater than the grid separation distance (Figure 3b). If so, then a 'rip' is possible at that location but suitably autocorrelated grids will overcome the problem (Figure 3c).
In some cases, however, transposition may occur between features that are not linked to each other (as with contours) and autocorrelation will not prevent damage to the topological integrity of the data after distortion. Thus, use of the model for contour perturbation, for example, is an ill- posed problem. On the other hand, there is no reason why the model could not be applied to provide z shifts to irregularly spaced point elevation data prior to interpolating contours or forming triangular facets.
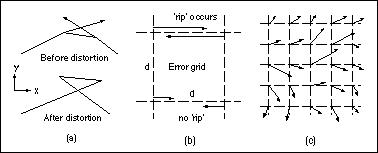
Figure 3. In (a), uncontrolled shifts between neighbouring error grid points can cause unacceptable 'rips' or transposition of features in the data set. In (b), 'rips' occur when the difference between neighbouring grid points is larger than their separation distance (d). In (c), autocorrelation is used to ensure 'rips' do not occur.
Initially it would appear that autocorrelation between error grid points is not required when creating the z shift grid, since point elevations are normally stored as attached attribute values and topological relationships are not constructed for point data. In addition, the z shift vectors would lie perpendicular to the plane of the error grid, unlike the x and y shift vectors which are coplanar, and the equivalent of 'rips' would not be expected to occur as long as the spacing of the error grids is less than the smallest distance between observed features and autocorrelation has been already applied to the x and y grids.
However, the authors' previous experience in perturbing elevations in DEMs has shown that autocorrelation is still required to prevent wild fluctuations occurring in the z shifts applied to neighbouring points if the distortions possess complete spatial independence (Hunter and Goodchild, 1994). For example, in a DEM with cells spaced 30m apart and z shifts being applied with a standard deviation of 20m, it can be quite common to observe one cell's elevation increase by 10-20m while its neighbour's decreases by a similar amount. Thus, two cells which might have originally had similar elevations now have a 20-40m difference in their heights even though they are only 30m apart. Our instinct and knowledge of spatial data tells us that such completely random variation is abnormal and should be avoided.
While some autocorrelation is required to achieve z shifts which appear 'natural' between neighbours, it cannot be automatically assumed to be equal to the amount needed for the x and y grids, since the circumstances in which it is applied are very different. In the case of the z grid, there is no exact method for determining the correct value of the parameter rho (such as, 'vary rho until there are no more rips'), and the authors have found that a series of z grids with rho values varying throughout the range 0 < rho < 0.25 needs to be created and applied to the point feature data set. By calculating, for each distorted data set, the mean difference between its elevations and the original observations, a graphical plot of elevation difference versus rho usually discloses a transition point in the curve that marks the point at which the z shifts cease being effectively constrained. This value of rho is then selected for autocorrelation of the z shift grids.
In Figure 4, the shifts at each grid point are represented by delta x and delta y, and D is the distance to the data point to be distorted. Inverse distance weighting ensures that grid points closer to the data point have greater effect than those that are further away. For computational efficiency, a minimum distance threshold should be set so that if an observed point is almost coincident with a grid point, then the shifts at that point are automatically adopted and the inverse distance weighing computation is not executed.
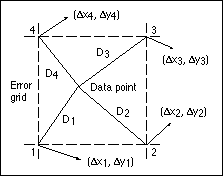
Figure 4. The x and y shifts for a point not coinciding with the error grid are calculated based on the weighted average of the four surrounding values, with closer grid points having greater weight than those further away.
Step 1:
Determine the separation distance required for the error grids and
the coordinate extent that the grids will need to cover. The number of
points needed in the grids will depend on these values.
Step 2:
Generate two error grids, initially with a value of rho = 0.
Step 3:
Test the grids for 'rips' and repeat Step 2 with increasing values of
rho until there are no more 'rips' remaining in either grid.
Step 4:
Adjust the autocorrelated grids to give the required spacing
between points and transform their coordinate origins to agree with the
data set being perturbed.
Step 5:
Taking each point in the observed data set in turn, calculate the
positional shifts in x and y to be applied based on the neighbouring error
grid values (with a minimum distance threshold being applied to detect
data points lying in close vicinity to error grid points).
Step 6:
Update the coordinates of each point using the shifts calculated in
Step 5.
Step 7:
Reconstruct the topology of the distorted grid, if applicable.
For operational purposes, the model could be widely used to determine the uncertainty of attributes derived from area and length estimates due to positional uncertainty in the original data. For instance, different versions of a road centerline database could be created to test the uncertainty in travel time and routing routines by running the same problem with perturbed data sets to assess which solutions have the best overall results. In other applications, more than one data set may need to be perturbed. For example, if the problem is to determine the economic effects of flooding based on different land uses, property values, soil types and flood zone ratings, then each vector data set could be perturbed according to its own error estimate before being overlaid to identify land which is at highest risk of flooding and the potential monetary loss. By running the model a number of times, the resultant variation in the financial amounts involved can be determined under conditions of uncertainty.
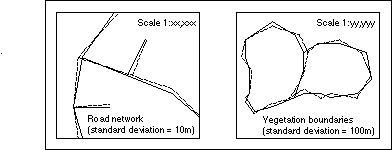
Figure 5. An educational application of the model would be for data producers to include visual samples of perturbed data sets in their data quality reports to help convey the meaning of their accuracy statistics.
The model may also be useful as a means of densifying or 'ungeneralising' data, if we assume that for certain types of data not only may the endpoints of lines be distorted, but also the positions of intermediate points along them. This approach would be unsuitable for perturbing land parcel boundaries, for instance, which are defined by their endpoints, however for data subject to natural variation it may provide a more realistic method of modeling their boundaries. This could be achieved by first placing additional vertices along each line segment (the usual means of densifying lines), and then applying the model to provide shifts at all node and vertex coordinates in the data (Figure 6).

Figure 6. In (a), only the endpoints of lines are distorted, whereas in (b) intermediate points along a line are independently distorted to provide a means of densifying the feature.
Goodchild, M.F., Guoqing, S. and Shiren, Y. 1992. 'Development and Test of an Error Model for Categorical Data'. International Journal of Geographical Information Systems, vol. 6, no. 2, pp. 87-104.
Hunter, G.J. and Beard, K., 1992. 'Understanding Error in Spatial Databases'. The Australian Surveyor, vol. 37, no. 2, pp. 108�19.
Hunter, G.J and Goodchild, M.F., 1994. 'Design and Application of a Methodology for Reporting Uncertainty in Spatial Databases'. Proceedings of the URISA '94 Conference, Milwaukee, Wisconsin, vol. 1, pp. 771-85.
Hunter, G.J., Goodchild, M.F. & Robey, M., 1994. 'A Toolbox for Assessing Uncertainty in Spatial Databases'. Proceedings of the AURISA '94 Conference, Sydney, Australia, pp. 367-79.
Moellering, H. (ed.), 1991. Spatial Database Transfer Standards: Current International Status (Elsevier: New York), 320 pp.