Soil properties vary laterally with topography resulting in patterns of soil development, a relationship that allows for prediction of soil attributes from landscape position. Slopes are often broken into five segments: summit, shoulder, backslope, footslope and toeslope. These delineations are usually determined using stereo photographs or field observations, based on elevation and profile curvature.
We are proposing new methods to automate this process and extend the utility of the classification for scientists and land managers. Continuous classification (fuzzy logic) methods and unsupervised (isodata) classification techniques were used to classify each pixel of a 10-meter resolution digital elevation model (DEM) according to its membership in a landform class. These classes were determined by the natural clustering of the data in attribute space. Attributes used for the classification were elevation, slope, profile and tangent (related to plan) curvature, compound topographic (wetness) index, and incident solar radiation. Because these factors are also important to soil forming processes, soil classes should nest within landforms. The unsupervised classification assigned pixels to one, and only one, landform class while continuous classification allocated relative class memberships to each pixel.
The ArcInfo GRID module was used for data manipulation, visualization and selected attribute derivation. The Solarflux AML (Rich and Dubayeh 1994) was used within GRID to calculate incident solar radiation and TAPES-G (Australian National University 1994) was used for hydrological parameters. GRID was used to perform the unsupervised classification and MacFuzzy (Ward et al. 1992) was used to perform the continuous classification.
Soil-landscape studies explore the relations between earth system processes, topography, and soil development. Soil scientists often rely on their knowledge of soil-topography-hydrology-vegetation relationships to infer soil types from landforms delineated on aerial photographs. This knowledge allows them to make assumptions about soil attributes and to identify areas for field verification.
The prevailing model for identifying landscape features delineates slopes into a limited number of segments. A common model for ridge and valley terrain uses five divisions: flat summit, convex shoulder, linear backslope, concave footslope and flat, alluvial toeslope (Ruhe and Walker 1968). Sometimes a delineation will also account for plan, or across-slope, curvature where stream channels converge or runoff diverges (Huggett 1975). Delineations may be made by interpreting stereopairs of aerial photography or contour maps.
The work presented here used a digital elevation model (DEM) to automate the classification of landforms for use in a soil-landscape study. We hypothesize that landforms derived from topographic features related to soil-forming factors will be correlated with the characteristics of the soils in those areas. The next stage of this research will investigate the soil-landform relationship.
The 50-hectare study site (Figure 1) is located in southwestern Wisconsin, in an area called the Driftless Area because it was not covered by glaciers during the most recent continental ice advance. It is a region of complex soils from many epochs of soil formation and movement. Topography is primarily narrow, alluvial valleys, steep slopes and broad ridges.
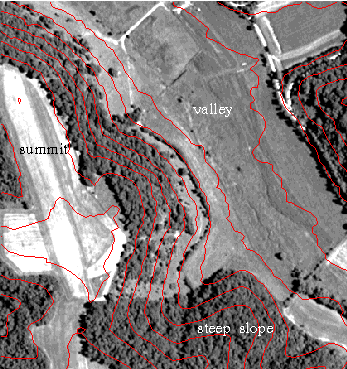
Figure 1. Orthophotograph of study site with 10-meter contour lines
Landforms were identified using three methods. The first method was a traditional approach--two soil scientists, experienced in the area, delineated the landforms using an airphoto stereopair (1:9600 scale, leaf-on). The other two methods were based on a DEM (10-meter horizontal and 0.3-meter vertical resolution) to analyze the landforms--an unsupervised classification method and a fuzzy-logic classifier. Each method used the same attributes to establish landform classes. Software used included ArcInfo GRID Rev. 7.0.2 (Environmental System Research Institute; Redlands, California); TAPES-G (Terrain Analysis Program for the Environmental Sciences-Grid, Version 6.0, Centre for Resource and Environmental Studies, Australian National University), a package designed for hydrological applications; and MacFuzzy, a continuous classification program (Ward et al. 1992). The primary platform was an IBM RS6000; in addition, a Sun workstation was utilized to run TAPES-G and a Macintosh Quadra 800 was used to run MacFuzzy.
Because this analysis is part of a soil-landscape study (the results of which will be used to predict soil properties), the attributes chosen are each important to soil formation by their impact on water and energy fluxes. In many landscapes, pedogenesis occurs in response to the way water moves through the landscape; therefore, the spatial distribution of topographic attributes that characterize these flow paths inherently capture the soil variability as well (Moore and Hutchinson 1991). The six attributes chosen to perform the classifications were: elevation, slope, profile curvature, tangent curvature (related to plan curvature), compound topographic index (CTI), and incident solar radiation.
Slope has been described as the single most important element of surface form since all surfaces are composed of slopes; gravitational force, controlled by slope angle, drives geomorphic processes (Evans 1972). Slope determines the speed of water flow and thus the velocity of material flowing down the slope or infiltrating into soils. Curvature of the slope is described as convex or concave and determines the pathway of the water and deposition points for alluvial material. Convex profile curvature indicates slope is increasing down-slope and is usually found near the top of hillslopes; concavity occurs in areas of decreasing slope, usually at the bottom of hillslopes. Convex plan or tangent curvature indicates divergent flowpaths while concave curvature identifies convergent flowpaths. Plan and tangent curvature are very similar; both are measures of across-slope curvature. Plan curvature is measured in a horizontal plane while tangent curvature is measured in a plane normal to the flowpath. It has been proposed that tangent curvature is a more appropriate attribute than plan curvature for studying flow convergence and divergence (Mitasova and Hofierka 1993).
The compound topographic index (CTI) has been used to describe the effects of topography on location and size of saturated areas (Moore et al. 1993). It is a refinement of upslope catchment area (area of land draining to a particular pixel) that better characterizes the spatial variability of soil properties due to surface hydrology (Moore et al. 1993). It is defined as ln(As/tanB), where As is the upslope catchment area and B is the slope.
Another important factor in soil formation is incident solar radiation (a function of aspect and slope), which increases the temperature of the soil thus affecting several facets of soil development. In this landscape, incident solar radiation influences microclimate, and so affects the physical (e.g., freeze-thaw characteristics), chemical (e.g., oxidation rates), and biotic (e.g., vegetation, microbiota) environment of the soil and soil surface.
Slope, profile and tangent curvature, and CTI were calculated using TAPES-G. The incident solar radiation was calculated using the SOLARFLUX AML (Rich et al. 1994), a GRID-based program developed for modeling solar radiation interception using a DEM. It uses slope, aspect and topographic hillshading to determine the solar radiation reaching each pixel.
The unsupervised classification of the data was accomplished using ISOCLUSTER and MLCLASSIFY in ArcInfo GRID. The ISOCLUSTER function uses an isodata clustering algorithm for defining natural groupings of data points in attribute space. It is a commonly used algorithm in satellite image classification in which spectral signatures from multiple wavebands (equivalent to attributes) are used to determine classes. In our case, we used the six defined attributes for each pixel to determine class compositions. The ISOCLUSTER function returns a signature file which can be used as input to a maximum likelihood classifier (MLCLASSIFY).
A major assumption of this type of classification is that a Gaussian distribution exists for the data; therefore, it is very important to analyze the histograms of the input attributes (STACKHISTOGRAM provides for easy viewing) . In some cases, a log transform is all that is needed to create a normal distribution of skewed data. Adequate distributions were attained for most of the attributes in this project (Figure 2); the slope data were log transformed. However, the elevation data were bimodal--violating the assumption of a gaussian distribution. We mitigated this problem by splitting the data set midslope (at the midpoint of the elevation data); as a result, each half of the scene had a normal distribution for this parameter. ISOCLUSTER and MLCLASSIFY were then run for each half of the dataset and the results combined (Figure 3).
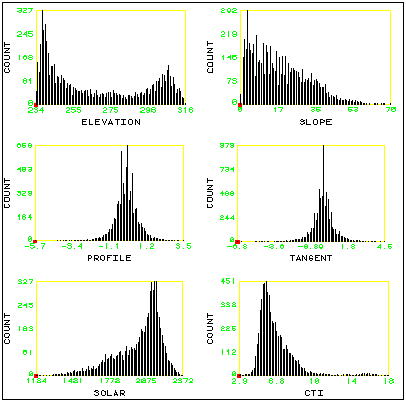
Figure 2. Histograms of untransformed DEM attributes used for classification
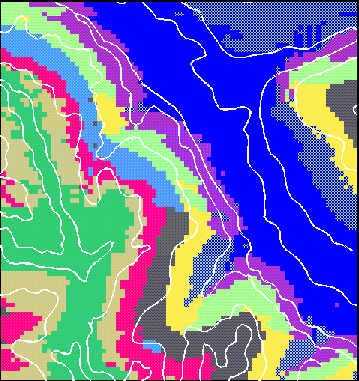
Figure 3. Ten landform classes created using the GRID functions ISOCLUSTER and MLCLASSIFY. Linework represents the manual landform delineation.
The isoclustering method assigned each data point to a particular class, i.e., each point was the member of one and only one class. This method may not provide a clear enough picture for some applications. Continuous, or fuzzy, classification techniques utilizing fuzzy k-means do not require data points to be exclusive members of one and only one class. Data points can be assigned partial membership in many classes. Continuous classification is based on fuzzy set concepts (Zadeh 1965), which provide a mathematical method of dealing with continuous data. These classification procedures have been used to classify natural resource phenomenon such as climate data (McBratney and Moore 1985), geologic data (Bezdek et al. 1984), and soils data (McBratney and DeGruijter 1992; Odeh et al. 1992; Slater 1994).
Continuous classification is accomplished through an iterative process in which individual data points are allocated class memberships using simple statistical measures of distance in attribute space (Ward et al. 1992). The membership value indicates how closely related an individual is to the centroid (attribute mean) of that class. We used MacFuzzy (Ward et al. 1992), which performs continuous classification using fuzzy k-means. It provides the option of allowing extragrades, which are data points poorly represented by any class; therefore, they have a low membership in most or all of the classes. Their characteristics are different enough from other points to warrant not being classified and are placed into an outlier class.
The amount of data associated with our study area created a prohibitively long processing time for the classification program because of the iterative processing. Comparable results were obtained by using a 25% subsample of the DEM-derived parameters as the input to MacFuzzy, which was used to determine the centroids for each class. From these centroids the class memberships were determined for the remaining data points based on an established method (McBratney 1994).
The classification program must be run several times to determine the optimum number of classes and the fuzzy exponent. The exponent determines the degree of fuzziness--the lower it is, the "harder" the classes (membership values of 1.00). If it is too high, the classifier may fail to converge or the classes may be too ambiguous. In this case the optimum number of classes for classifier performance was fifteen with a fuzzy exponent of 1.30. The memberships for each class were placed into separate ArcInfo grids for viewing and manipulating. Based on our knowledge of the landscape, we combined several similar classes to create nine landform classes and an extragrade class (Figure 4).
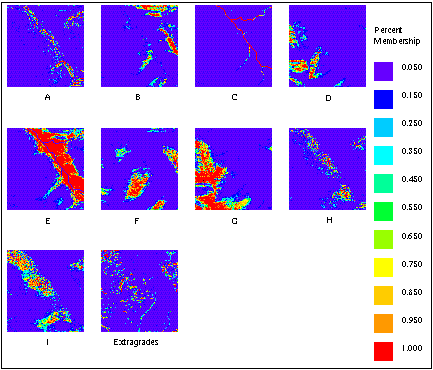
Figure 4. Continuous landform classes A - I and extragrades. Shade color represents percent membership in a particular class for each pixel.
The results of both classification techniques were compared to the manual airphoto delineation (Figure 3). All of the methods picked up significant features such as the valley bottom, terraces, convex shoulder slopes, and the summit. The automated methods seemed to have a slighter higher resolution of detail, which was due in part to the viewing system employed (mirror stereoscope) for the manual delineation. The automated methods also differentiated features based on aspect, so that north-facing slopes were in a different class from otherwise-similar south-facing slopes. Some discrepancy in boundaries exist; the use of leaf-on photography for the manual delineation made it somewhat difficult to identify features on the wooded slopes, and manual delineation of airphotos relies on subjective judgment.
Unsupervised and fuzzy classification methods both produce results that can aid soil scientists and others interested in soil-landscape processes. A few caveats apply. Some knowledge of the landforms in question is necessary to evaluate the efficacy of the results of either method. Also, care should be taken in the choice of attributes; they should reflect the nature of the landscape and the phenomenon being studied.
Each classification method has its advantages and disadvantages. The unsupervised classification provides summary information about landforms in a relatively quick manner; results are easy to view and transform into polygonal form recognized by soil scientists. However, the "hard classification" lacks complete information about transition zones, and particularly the variability inherent therein. Classification performance may depend on distribution of the data; failure to normalize a non-gaussian distribution of an attribute may give erroneous results. The continuous (fuzzy) classification provides much additional information on each point, which may be useful for detailed understanding of landscape processes. But it is a more time-consuming method and the results are not as easily visualized and directly usable by field pedologists.
The unsupervised classification may be best suited to identifying landforms, or areas of rapid change, which may require more intensive sampling to obtain a complete picture of the soils in an area. Because the fuzzy classification provides more complete information about the landscape characteristics, it may be better suited for the prediction of soil properties in sparsely sampled areas and to further understanding of underlying soil-landscape processes.
The work report in this manuscript was supported in part by a grant from the National Science Foundation (SES-0210093).
Bezdek, J.C., R. Ehrlich and W. Full (1984). FCM: the fuzzy c-means clustering algorithm. Computers & Geosciences 10: 191-203.
Evans, I.S. (1972). General geomorphometry, derivatives of altitude, and descriptive statistics. In Chorley, R.J., ed. Spatial Analysis in Geomorphology. London: Methuen & Co. Ltd. 17-90.
Huggett, R.J. (1975). Soil landscape systems: a model of soil genesis. Geoderma 13: 1-22.
McBratney, A.B. (1994). Allocation of new individuals to continuous soil classes. Australian Journal of Soil Resources 32: 623-633.
McBratney, A.B. and J.J. DeGruijter (1992). A continuum approach to soil classification by modified fuzzy k-means with extragrades. Journal of Soil Science 43: 159-175.
McBratney, A.B. and A.W. Moore (1985). Application of fuzzy sets to climatic classification. Agricultural and Forest Meteorology 35: 165-185.
Mitasova, H. and J. Hofierka (1993). Interpolation by regularized spline with tension: II. Application to terrain modeling and surface geometry analysis. Mathematical Geology 25(6): 657-669.
Moore, I.D., P.E. Gessler, G.A. Nielsen and G.A. Peterson (1993). Soil attribute prediction using terrain analysis. Soil Science Society of America Journal 57: 443-452.
Moore, I.D. and M.F. Hutchinson (1991). Spatial extension of hydrologic process modelling. International Hydrology and Water Resources Symposium, Perth, Australia, 803-808.
Moore, I.D., A. Lewis and J.C. Gallant (1993). Terrain attributes: estimation methods and scale effects. In Jakeman, A.J., M.B. Beck and M.J. McAleer, ed. Modelling Change in Environmental Systems. Chichester: John Wiley & Sons Ltd. 189-214.
Odeh, I.O.A., A.B. McBratney and D.J. Chittleborough (1992). Fuzzy-c means and kriging for mapping soil as a continuous system. Soil Science Society of America Journal 56: 1848-1854.
Rich, P.M., W.A. Hetrick and S.C. Saving (1994). Modelling topographic influences on solar radiation: a manual for the SOLARFLUX model (Draft). Lawrence, Kansas: University of Kansas.
Ruhe, R.V. and P.H. Walker (1968). Hillslope models and soil formation: II. Open systems. Transactions of the 9th Congress of the International Soil Science Society, Adelaide, 551-560.
Slater, B.K. (1994). Continuous Classification and Visualization of Soil Layers. Ph.D. dissertation, University of Wisconsin-Madison.
Ward, A.W., W.T. Ward, A.B. McBratney and J.J. Degruijter (1992). MacFuzzy: A program for data analysis by fuzzy k-means. Glen Osmond, S. Australia: CSIRO Division of Soils.
Zadeh, L.A. (1965). Fuzzy sets. Information and Control 8: 338.