SD Lynch and RE Schulze
ABSTRACT
Daily rainfall records are of paramount importance when performing hydrological investigations at a daily or monthly time scale. This paper will discuss the two aspects of daily rainfall records, namely, creating continuous records and estimating areal rainfall. A plethora of techniques is available if the hydrologist needs to estimate daily areal rainfall for a small area or if the hydrologist needs to estimate missing values for the occasional rain-gauge position. The hydrological fraternity needs a suite of automated techniques to describe areal rainfall for a large area or to estimate missing rainfall for a large number of rain- gauge positions.
The hydrologist is often faced with the problem of choosing a technique to estimate areal daily rainfall and a large amount of valuable time is then spent on deciding which techniques, hardware and software will meet their requirements. Southern Africa, for example, covers an area of approximately one million square kilometres and results in approximately 800 000 one minute by one minute (1600 by 1600 metres) of a degree pixels. It is therefore important to note that the spatial representation for one year of gridded daily rainfall for Southern Africa will result in approximately 292 million pixels. Detailed research is therefore needed to advise the user on which interpolation technique will suit his hardware, software and time requirements.
This paper summarises some well-documented techniques and also gives detailed results for the new proposed techniques that include inter alia regression, interpolation, kriging and averaging techniques. The results will be in the form of a table displaying the amount of hardware and human time and the type of hardware and software required.
Rainfall at a daily time scale is the single most important parameter in hydrological computer simulation models and researchers are often faced with the problem of which interpolation technique to use when determining the spatial distribution of daily rainfall from rain-gauge positions.
A plethora of techniques exists that allow the user to convert point measurements to a surface that describes the spatial pattern over an area. Geographic Information Systems (GIS) provide the user with an array of interpolation techniques to choose from. In this paper we will discuss some well-known interpolation techniques and provide the reader with a table summarising the results obtained when interpolating point estimates of daily rainfall onto a rectangular surface.
The study area is approximately 10735 km**2 in size and is located between the latitudes of 29 and 30 degrees south, and the longitudes of 30 and 31 degrees east, in the province of KwaZulu-Natal, South Africa (Figure 1).
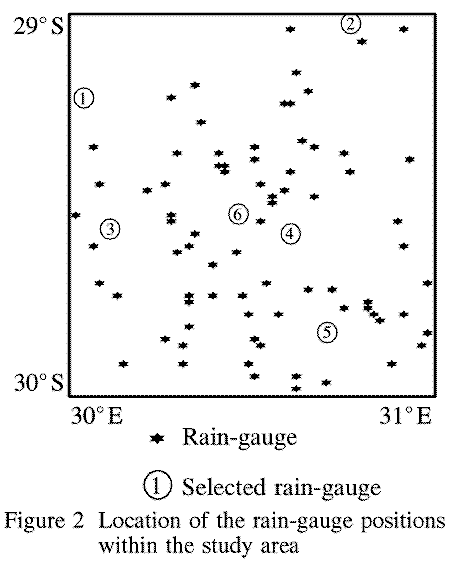
There are 90 rain-gauges in the study area (Figure 2) varying from a dense to a sparse spatial distribution.
The availability of gridded altitude and gridded monthly rainfall at a scale of 1' by 1' of a degree, approximately 1600 by 1600 m, (Dent, Lynch and Schulze, 1988) led to the acceptance of this as the pixel size for this project.
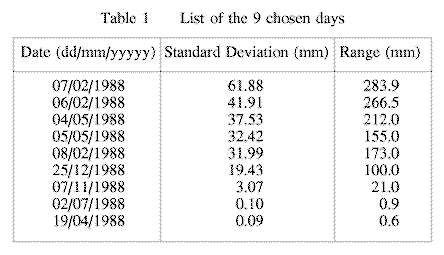
The KwaZulu-Natal region experienced abnormally high rainfall in 1988 with some rainfall stations reporting in excess of 280 mm in one day. The year 1988 is an ideal period to use for the comparison of the different interpolation techniques. As many of the interpolation techniques use vast amounts of computer time it was decided to select only a few days in 1988 as input data sets. The standard deviations of the daily rainfall for each day for the whole study area were determined and 9 days, with high, average and low standard deviations, were chosen (Table 1).
The most common method used for interpolation onto a regular grid from random spaced points is based on the computation of a weighted average (Equation 1) of a representative sample of points in the vicinity of a grid node. The distance weighting techniques are simple to program and can be adapted to run on virtually any hardware platform and it was therefore decided not to use the techniques supplied by ArcInfo.

In this method weights are calculated depending on the distances between the grid node being estimated and the control or rain- gauge positions. The weighting function for Equation 1 is given by;
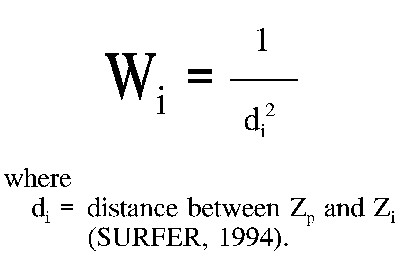
In this method weights are calculated using a search radius and the weighting function for Equation 1 is given by;
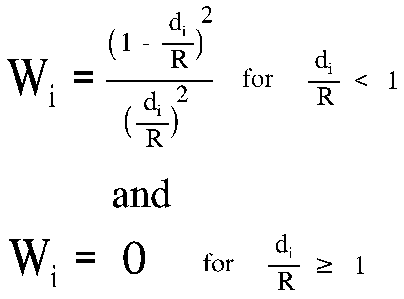
The choice of R depends on the density of the data points and should be chosen so that the sampling circle includes at least five sample points (Yoeli, 1975).
This method makes use of the assumption that the distribution of daily rainfall is similar to the distribution of median monthly rainfall. In this method (Schafer, 1991) the daily rainfall amounts at each rain-gauge position are expressed as a percentage of the median monthly rainfall at that point for the day of the month in question. These percentages are then interpolated onto a rectangular grid using a two dimensional interpolation technique (SACLANT, 1979). After this interpolation has been performed the rectangular grid of percentages is then multiplied by the gridded median monthly rainfall surfaces (Dent, Lynch and Schulze, 1988) to produce surfaces of daily rainfall.
Geographers often use Thiessen polygons to model or approximate the zones of influence around points. Immediately surrounding the Thiessen polygon enclosing a specific rain-gauge are other Thiessen polygons, each which also encloses a single rain-gauge. To achieve computational efficiency, elaborate sorting and searching algorithms need to be developed and this led to use of the Thiessen polygon method of the ArcInfo system. The assumptions that the polygons represent flat plans results in a very crude approximation of the surface (Davis, 1986).
This is a two dimensional interpolation technique that consists of an initial assignment of values to the grid points followed by a process whereby the grid values are iteratively improved until the surface through the original data points has obtained a satisfactory state of smoothness (SACLANT, 1979).
The KRIGING routine (ArcInfo, 1991) interpolates a set of points using either a spherical, or a circular, or an exponential, or a gaussian, or a linear, or a universal (linear drift), or a universal (quadratic drift) semi-variogram model. Kriging is not an exact interpolation and regression method and the residual value at the known data points can therefore be used as a possible method to determine which semi- variogram model to use. The KRIGING routine (ArcInfo, 1991) was used to generate surfaces for each of the 9 selected days (Table 1) and the root mean square errors (RMSE) between the known input data points and the interpolated values were determined (Table 2) to assist in choosing which semi-variogram model to use.

The universal kriging with linear drift has the lowest RMSE and was therefore decided upon as the semi-variogram model to represent the Kriging interpolation technique in this research.
The scope of this research is not to determine the best or most suitable interpolation technique but to determine what differences there exist between the different interpolation techniques. The classic method of temporarily discarding a point from the data set and then interpolating the data set to be able to compare the discarded value to that of the interpolated value at that point falls short if similar techniques are being compared (Isaaks and Srivastava, 1989).
The classic statistics of inter alia mean, median, standard deviation and skewness do not lend them to the comparison of gridded surfaces as can be illustrated in the following example. If one had to compare a surface to a mirror image of that same surface, the classic statistics would be the same indicating that the surfaces are the same. Clarke (1995) suggests that the best method to use when comparing geo-referenced surfaces is a grouping method to determine how the pixel values differ at similar locations. The percentage of the pixels that are within 10% of the range for each of the selected days (Table 1) are averaged (Table 3). The Thiessen interpolation technique (ArcInfo, 1991) is the only technique that does not have an average grouped value of more than 90% when compared to the other techniques.

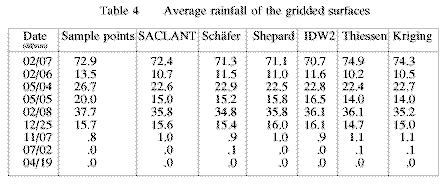
Engineers and hydrologists often need the areal daily rainfall estimates as input into hydrological computer simulation models. If there is a reliable, complete and representative record of daily rainfall within a catchment or sub-catchment then there is no need to use these interpolation techniques. What often happens is that the rainfall distributions vary within a catchment or sub-catchment and the researcher then employs an averaging procedure to estimate a representative daily rainfall. The average daily rainfall of the gridded surfaces are determined for the area in question for each of the selected 9 days using the different interpolation techniques (Table 4). The fact that these average values are very similar suggests that there is hardly any difference and therefore the averaging of the rainfall amounts, without any interpolation, would be sufficient if only an average daily value were needed.
Incomplete daily rainfall records are also one of the many problems that are encountered when daily hydrological computer simulation models are used. The above mentioned interpolation methods can also be used to approximate the missing rainfall amount.
The SACLANT, Schafer, Shepard and IDW2 interpolation techniques are simple to translate into computer code to run on virtually any computer hardware. Their execution time is also fast as they do not allow the user the flexibility of the ArcInfo interpolation routines like Thiessen and Kriging (Table 5).
Some advantages and disadvantages of the different interpolation or griding methods are; SACLANT can run on virtually any hardware platform and the processing time is fast, Schafer can run on virtually any hardware platform and the processing time is fast, but this technique relies on the availability of gridded median monthly rainfall, Shepard can run on virtually any hardware platform and the processing time is fast, and this method does not tend to generate "bull's eye" patterns (SURFER, 1994), IDW2 can run on virtually any hardware platform and the processing time is fast, but this method tends to generate "bull's eye" patterns of concentric contours around the data points (SURFER, 1994), Thiessen needs complex search and programming procedures, the processing time is slow and the spatial distribution of the data set needs to be dense, Kriging semi-variograms need to be analyzed before this technique can be used and sophisticated programs are also needed.
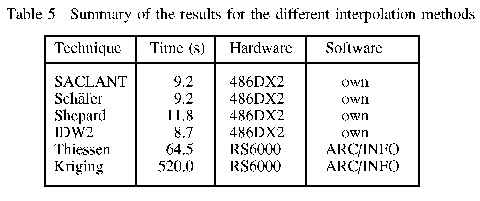
Table 5 lists the computer time in seconds required to interpolate a single (1 day) rectangular grid of 61 rows by 61 columns from a data set of 90 points (Figure 2).
The rainfall data that formed the basis of the study was supplied primarily by the South African Weather Bureau, and the Department of Agriculture and Water Supply and their contributions are acknowledged gratefully. The staff of Geographic Information Management Systems (GIMS) are also acknowledged for their assistance in using the ArcInfo software. Finally the Computing Centre for Water Research is acknowledged for the provision of computing facilities and for assistance with computing.
ArcInfo ,1991. Cell-based modelling with GRID. Environmental Systems Research Institute, Inc., Redlands, USA.
Clarke, GPY, 1995. Personal communication. Dept. Biometry and Statistics, Univ. of Natal, Pietermaritzburg, South Africa.
Davis, JC, 1986. Statistics and Data Analysis in Geology. John Wiley & Sons, New York.
Dent, MC, Lynch, SD and Schulze, RE, 1988. Mapping mean annual and other rainfall statistics over Southern Africa. Univ. of Natal, Dept. Agric. Eng., ACRU Report 27, Water Research Commission, Pretoria, South Africa. Report No 109/1/89.
Isaaks, EH and Srivastava, RM, 1989. Applied Geostatistics. Oxford University Press, New York.
SACLANT (NATO) ASW Research Centre, 1979. Spezia, Italy.
Schafer, NW, 1991. Modelling the areal distribution of daily rainfall. Unpubl. M.Sc.Eng. thesis, Dept. Agric. Eng., Univ. of Natal, Pietermaritzburg, South Africa.
SURFER for Windows, User's Guide, 1994. Golden Software, INC., Golden, Colorado, USA.
Yoeli, P, 1975. Compilation of data for computer-assisted relief cartography. Pg 352-367, Davis, JC and McCullagh, MJ (Eds): Display and Analysis of Spatial Data (NATO Advanced Study Institute). John Wiley & Sons, London.
Steven D Lynch and Roland E Schulze