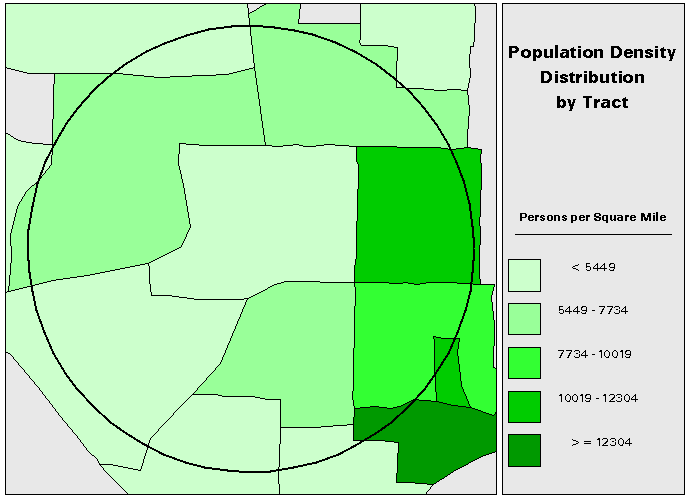
Figure 1. Population Density Distribution by Tract
Erik Shepard, Doug Atkinson, and Anita Russo; Information Technology Outreach Services, The University of Georgia
Areal interpolation weights data values for a partial polygon proportionally to the ratio of partial polygon area to complete polygon area. This implicitly assumes that the data are uniformly distributed throughout the polygon. This is usually not the case for population related data. A knowledge of the actual populations of subpolygons comprising the original polygon can be used to approximate varying density. The areal weight for each subpolygon is first calculated and then used to weight the associated population value. The weighted populations are then summed and the ratio of partial polygon population to complete polygon population is calculated. Finally, the population ratio is used to interpolate the population related data value of interest, such as mean income, for the original polygon. This improved method assumes that the data are uniformly distributed in the subpolygons, which is a better assumption than uniform distribution in the original, larger polygon. Increasingly fine resolutions of population data will better approximate varying population density in the original polygon. The method for population-based interpolation is written in ARC Macro Language and runs under ArcInfo and ARCPlot. The purpose of this paper is to address the appropriateness of using population information to interpolate population related data for partial polygons.
Data in geographic information systems frequently suffer from several problems that are inherent in the generalization of data. Burt and Barber (1996) describe four of these problems as the boundary problem, the scale problem, the problem of modifiable areal units, and the problem of pattern. In the realm of demographic data, such as the data collected by the United States Census, one of these problems is quite evident: the problem of modifiable areal units. According to Bailey and Gatrell (1995), "any results we obtain from analyses of area aggregations may be conditional upon the set of zones we are presented with, a problem which is often referred to as the modifiable areal unit problem."
The United States Census defines a nested classification scheme whereby counties are exhaustively divided into tracts. Tracts are made up of block groups, which are themselves a collection of blocks. This classification, even before data are collected, already imposes a somewhat arbitrary division of space; that is, a modifiable areal unit. Although the tract and block group subdivisions were originally designed conceptually to contain roughly equal population sizes and equal demographics, in practice the daily fluctuations of human populations makes this classification hard to maintain. The modifiable areal unit problem forces the results of any study performed upon the data to be dependent upon not only the data themselves, but upon the organization of the data as well. Moreover, data collected by the Census are usually aggregated at some level (such as tracts) which presents a scale problem. Processes that manifest themselves at a lower level are hidden by the aggregation.
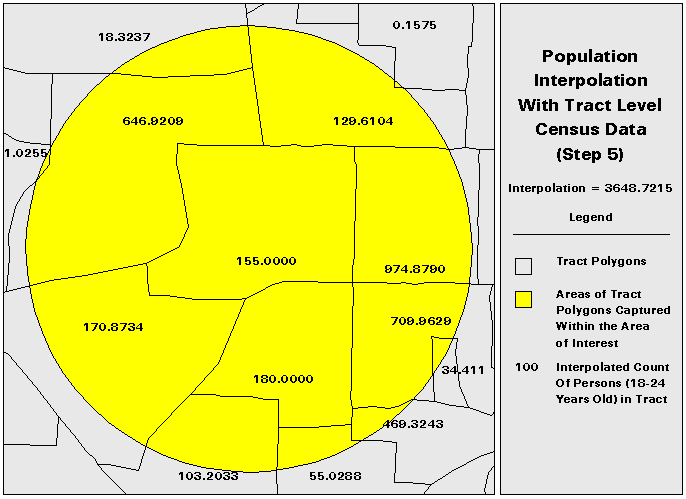
Consider, for example, population density within a circular area of interest (AOI) with a radius of one mile. An examination of density aggregated at the tract level (figure 1) suggests a very simple picture of density distribution where the rightmost section of the AOI has the highest density values while the top of the AOI has middle density values and the center and bottom sections of the AOI have the lowest density values.

An examination of the same data aggregated instead at the block level (figure 2) suggests a much more complex picture where most of the AOI has low density values with the highest values distributed randomly (rather than clustered) throughout the AOI.
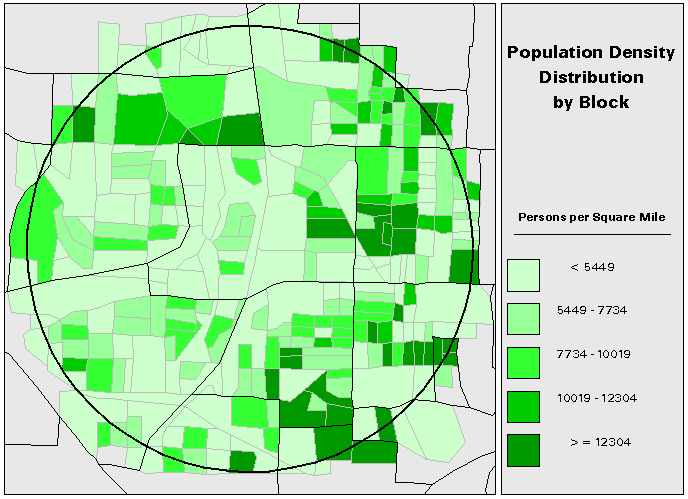
The modifiable areal unit problem and the scale problem both complicate the evaluation of an AOI which does not follow the boundaries of collected data and for which the data in question must be somehow interpolated. There are many methods in the literature which address this problem. The remainder of this paper will examine the strengths and weaknesses of a few of these techniques and will then suggest a new method for interpolating polygon data that are correlated with population. The circular AOI in the previous example will be used with 1990 Census counts of persons from 18-24 years of age aggregated at the tract and block group levels to illustrate examples. Block level population data, also from the 1990 Census, will be used to calculate population factors in the population based interpolation.
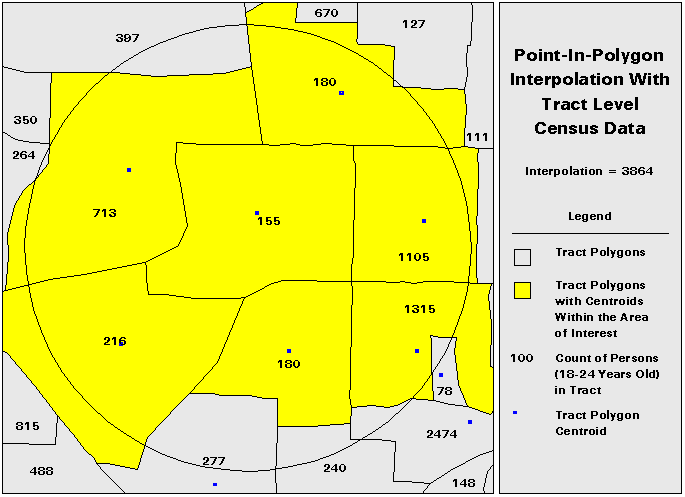
Interpolating Polygon DataAn approach to interpolating polygon data is referred to as point-in-polygon. In this technique, data values for polygons whose centroids fall within the AOI are used to interpolate the data value for the complete AOI. The principle advantage of this technique is that it is relatively simple to calculate; indeed there are many solutions to the point-in-polygon problem in the literature. The obvious disadvantage to this technique is its coarseness. Figure 3 illustrates an application of the point-in-polygon technique. Note that this technique suffers from a modifiable areal unit problem due to the fact that polygon centroids are based upon the polygons used to collect the data. Therefore, the interpolation values will vary with different data collection schemes. For example, the interpolation value for the tract level data in figure 3 is 3864. The interpolation value for the same data at the block group level is 4624 - a difference of nearly 800 in the estimation.
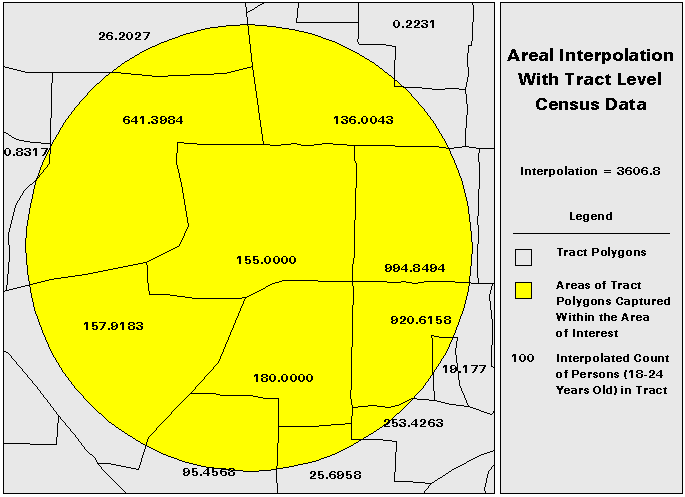
A better approximation, known as areal interpolation, is to take a ratio of the AOI polygon area to data collection polygon area and to use this to weight the data. Figure 4 illustrates application of the areal interpolation. This is probably the most commonly used method, owing predominantly to the simplicity of calculation and the improved accuracy over the point-in-polygon technique. This approximation, although better than the point-in-polygon interpolation, still suffers from some drawbacks. Chief among these is the implicit assumption that the data are uniformly distributed throughout the data collection polygon (DCP). This is usually not the case, especially in demographic data. This technique also suffers from a modifiable areal unit problem due to the fact that ratios of areas of polygons vary with different polygons. The interpolation value for the tract level data in figure 4 is 3606.8 while the interpolation value for the data at the block group level is 3692.3956. Although this variation is not as drastic as the variation in the point-in-polygon technique, it still represents a difference of nearly 100 in the estimation.
There are many other methods which can be used to interpolate as well, but these are beyond the scope of this paper. Most of these techniques have the advantage of improved accuracy but suffer from performance issues due to their iterative nature.
Population Based InterpolationAs indicated above, the areal interpolation suffers from the assumption that the data are uniformly distributed throughout the DCP. Any underlying heterogeneity is masked. The problem, then, is to interpolate the polygon data in such a way as to preserve the underlying structure.
The best way to accurately model the distribution of a population is to obtain data on that population itself. Obviously, the better the resolution of the population data, the more accurately the population distribution can be modeled. This modeled population distribution can be used to interpolate the data of interest.
With finer resolution population data, representative populations for each population data subpolygon can be calculated, disaggregating portions of subpolygons (if necessary) by interpolating areally. If these subpolygon populations are summed and divided by the total population for the DCP, an interpolation factor which reflects the proportion of population in the DCP is generated. This interpolation factor can then be used to disaggregate the DCP data. The sum of the interpolated DCP data for all DCPs in the AOI is the interpolation value.
The general algorithm is straightforward:
1. Divide the DCP polygons into subpolygons for which population data are available. (Figure 5)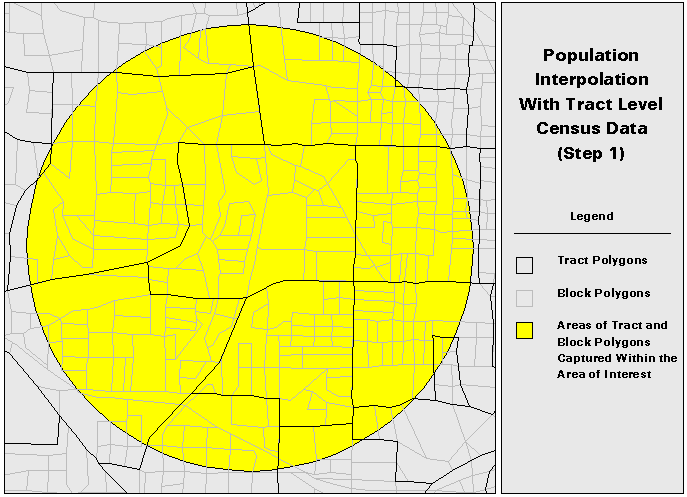
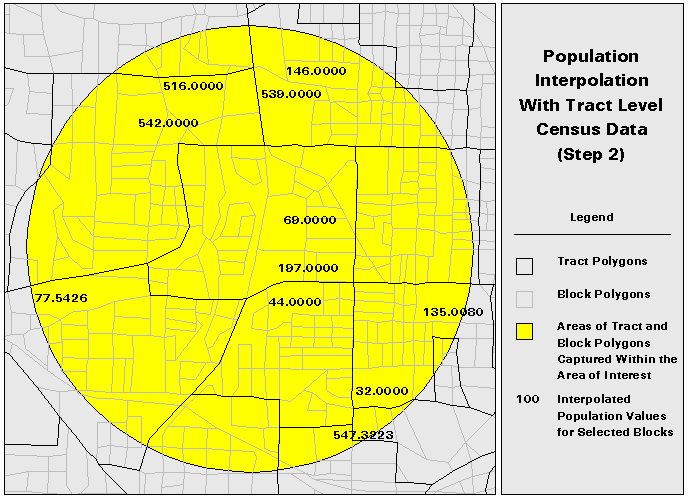
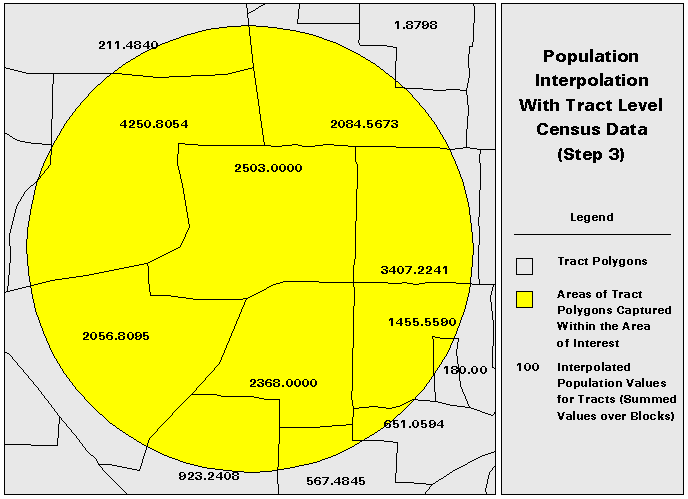
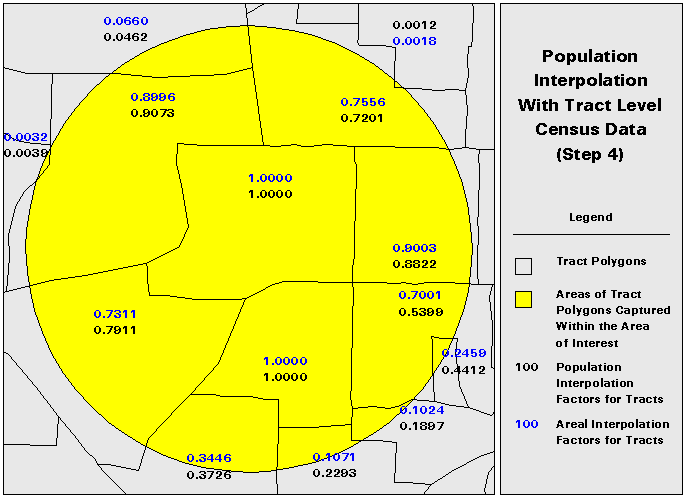
This technique still relies upon an areal interpolation for any of the subpolygons that are transected by the AOI polygon. However, the subpolygon data is at a finer resolution than the DCP data. Although population will still not be uniformly distributed in the subpolygons, the distribution should be closer to uniform in the subpolygon than in the data collection polygon.
There are several points which should be mentioned about this procedure. First, this procedure suffers from not one but two modifiable areal unit problems - first from the aggregation of the DCP data and second from the aggregation of the population data. Using the best resolution data possible (particularly in the population data) should minimize the modifiable areal unit impact.
Second, this technique cannot be used in situations where the data to be interpolated is not correlated with some population or in situations where the population data available are not of better resolution than the data to be interpolated. Due to the areal interpolation of the population data, population data of the same resolution as the DCP data will result in the technique yielding exactly the areal interpolation of the DCP data with no improvement.
Third, this technique is not as efficient as a traditional areal interpolation due to the necessary areal interpolation of the population data at a fine resolution and the subsequent interpolation using the interpolated population data. The population interpolation (with block level population data) takes an average of 5 times as long as the corresponding areal interpolation. For extremely large AOI polygons, the population interpolation can take much longer than the areal interpolation.
Lastly, population data are continuously changing. Projections of later DCP data based upon earlier population data (and hence population distributions) may not be appropriate. Some caution is advised when using population data and DCP data collected at different times.
Table 1 summarizes the results for the AOI used in the examples for point-in-polygon interpolations of block group and tract level data, areal interpolation of block group and tract level data, and population interpolation of block group and tract level data with block, and block group level population data.
| Interpolation Method | Interpolation Value | |
| Tract Level Data | Point-In-Polygon | 3684.0000 |
| Areal | 3606.8000 | |
| Population (Block Group Level Population) | 3687.3657 | |
| Population (Block Level Population) | 3648.7215 | |
| Block Group Level Data | Point-In-Polygon | 4624.0000 |
| Areal | 3692.3956 | |
| Population (Block Level Population) | 3667.4177 |
The values for the population interpolations also vary due to the modifiable areal unit problems, but not as greatly as the point-in-polygon and areal interpolations (the variance here is only about 40 in the estimation).
To evaluate the improvement of the population interpolation over the areal interpolation, 70 circular AOI polygons were generated ranging from a 1 mile radius to a 100 mile radius. Areal interpolations at the block group and tract level were then generated together with population interpolations at the block group and tract level with block group and block population data. Areal interpolations of tract level data were then compared with population interpolations of tract level data using block group and block population data. Likewise, areal interpolations of block group data were compared with population interpolations of block group data using block population data. Table 2 summarizes the mean differences for each of the AOI sizes.
| Tract Level Data | Block Group Level Data | ||
| AOI Size | AREA vs POP (BG) | AREA vs POP (BL) | AREA vs POP (BL) |
| 1 Mile Radius | 21.1072 | 23.8162 | -1.2558 |
| 5 Mile Radius | 20.7734 | 227.9367 | 207.4622 |
| 10 Mile Radius | -10.9693 | -428.6546 | -431.3140 |
| 20 Mile Radius | 151.7632 | -389.2268 | -551.8002 |
| 25 Mile Radius | 252.8210 | 317.0413 | 92.4306 |
| 50 Mile Radius | 638.3625 | 940.4615 | 299.3910 |
| 100 Mile Radius | 762.3927 | -6180.4908 | -6893.9754 |
Although the population interpolation technique is more computationally intensive than the areal interpolation or point-in-polygon interpolations, it yields a fairly large improvement. Using tract level data with block population data, for instance, the mean difference between the areal interpolation and the population interpolation was aproximately 225 persons for the 5 Mile Radius AOIs. For the 100 Mile Radius AOI, the difference between the areal interpolation and the population interpolation was nearly 6200 persons.
The impact of the improvement increases in proportion to the number of polygons.This is logical since the more polygons in an AOI, the more polygons that will be interpolated. Unfortunately, processing time also increases in proportion to the number of polygons. If processing time is not a factor, the population interpolation method should be used. However, if processing time is a factor, the areal interpolation should still yield reasonably good results in less time.
References and Acknowledgements