Avi Ostfeld, Kevin E. Lansey, Yigal Salingar, and Thomas Maddock III

This paper describes the development of a decision support system for the Lake Hula restoration site in northern Israel. The decision support system is termed HANDSS (Hula Aggregated Numerical Decision Support System), and is designed as an end user interface that is comprised of three main components: (1) ArcView to interactively prepare and modify GIS data sets, (2) The Department of Defense Groundwater Modeling System (GMS) to analyze subsurface flow regimes, and (3) an LP (Linear Programming) management model to select optimal water allocation alternatives.

In the late 1950s Lake Hula and its surrounding swamps, located in the northern part of Israel, were drained by the Jewish National Fund (JNF) giving over most of the area to agriculture. This was a Zionist action aimed at sanitizing the malaria-infested in the Hula valley and turn the area over into suitable land for agriculture.

Soon after the project completion it looked like a great success as it allowed cultivation of new fertile land and drove the economy in the region to flourish. However, during the last two decades it became evident that there is an over-widening gap between the project expectations and its consequences. The interference in the natural system of the Hula valley caused series of physical and biogeochemical irreversible problems: the peat soils decomposed and settled leading to deterioration of the soil quality and narrowing by 10-20 % the land suitable for cultivation; peat fires accelerated causing dust storms; poisonous weeds spread out; field mice multiplied; indigenous fauna and flora disappeared; water bird population declined; and the quality of water in Lake Kinneret has been impaired.

By the end of the 1980's it became evident that a rapid action of restoration is essential. With this in mind a restoration plan has been established recognizing five different major systems in the area (Shaham, 1995): (1) The agricultural system that includes the farmers that live from cultivating the land, (2) the national water system that includes the Jordan River that flows through the drained area to Lake Kinneret; (3) the unique flora, fauna, and landscape that failed to preserve after the drainage of the Hula swamps; (4) the water supply and drainage system in the region, and (5) the organizational system that initiates and regulates the activities within the area.

It was obvious that in order to reach a restoration engineering scheme, a compromise among the groups involved is required (Shaham, 1995). The compromise solution that was agreed upon is an agro-tourism alternative that incorporates agriculture, tourism, and preservation of the flora, fauna, and landscape.

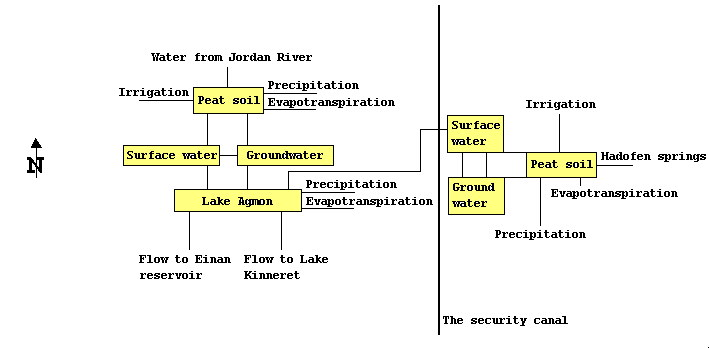
The guiding principle of the restoration scheme is to raise and maintain a high water table in the Hula valley area using waters from the Jordan River in the west, spring water from the Golan foothills in the east (i.e. Hadofen springs), and internal drainage waters of the peat soils. This is implemented by a grid of constructed drainage canals whose water levels are controlled by a set of hydraulic structures, and by intensive cropping and irrigation of the land. Managing the water levels within the drainage canals, and the intensive cropping and irrigation, should minimize the decomposition and subsidence of the peat soils, ensure a year round green cover of the area, allow the farmers to continue the cultivation of their fields, and create an artificial lake (termed the Agmon) at the center of the area, that is intended to serve for tourism and recreation purposes. A box diagram of the structure of the Hula valley restoration site is shown in Fig. 1.

Fig. 1: A box diagram of the structure of the Hula valley restoration project

To fulfill the above tasks an R&D program has been initiated by the JNF with the following objectives (Shaham, 1995): (1) Closure of gaps in understanding the processes involved in the regional surface water and the subsurface water bodies in the area with respect to water quantity and quality, (2) development and adaptation of tourism-oriented land and water habitats to enhance the site's economic potential, (3) adoption of a balanced ecological management scheme for the regulation of harmful natural populations (e.g. mosquitoes, field mice, weeds), and (4) development and adoption of "environmental-friendly" agriculture in the peat lands.

To accomplish the R&D objectives a three year research program was established in the following areas: (1) Research of the peat lands, (2) research in the area designated for tourism, (3) water research: quantity and quality in the Agmon and in its peripheral canals, and research of the Hula valley hydrology regime, and (4) establishment of a GIS data base for the Hula valley restoration project.

The GIS data base stores soil, groundwater, water quality, and engineering infrastructure data of the project. The GIS is planned to operate as a continuously updated tool that gets its input from research activities, and from continuously measurement plans.

The outcome of the three year research program is intended to provide the knowledge for the managers, regulators, and consultants involved in the Hula valley restoration project, on how the system functions, and how it should be effectively managed, such that the objectives of the restoration project will be accomplished. The research problem we are facing is how to integrate the existing knowledge outcome from the different research activities with the GIS data base in an overall decision support system that will enhance the operators in selecting effective overall management schemes.

The decision support system we are currently developing and reporting hereafter is for the optimal allocation of waters among the Lake Hula site consumers subject to constraints on water levels within the irrigated lands (peat and not peat soils), and water quality at the Agmon Lake.

The decision support system is termed HANDSS (Hula Aggregated Numerical Decision Support System), and is designed as an end user interface that is comprised of three main components: (1) ArcView to interactively prepare and modify the required data sets, (2) The Department of Defense Groundwater Modeling System (GMS) to analyze subsurface flow regimes, and (3) an LP (Linear Programming) management model to select optimal water allocation alternatives. The front interface screen of HANDSS is shown in Fig. 2.

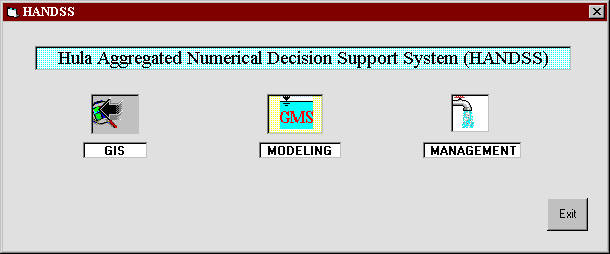
 Fig. 2: Main components of the Lake Hula decision support system

The GIS coverages (established using ArcInfo and displayed with ArcView) for the Lake Hula project that are used in HANDSS are shown in Fig. 3-6. The GIS data base has been constructed by the JNF GIS Israeli group directed by Dr. Yigal Salingar.

Fig. 3 is a map of the project site, showing its boundaries, its grid of drainage canals, the location of the hydraulic structures with which the groundwater levels in the area are controlled, and the Agmon Lake.

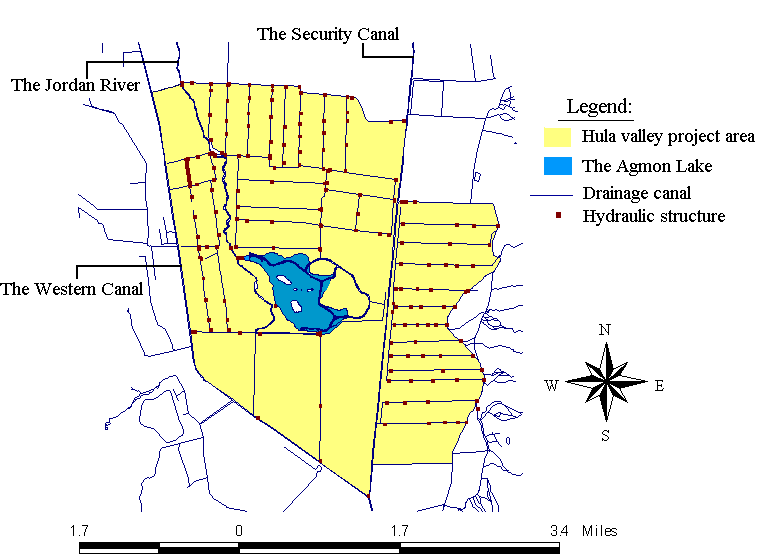
Fig. 3: General layout of the Lake Hula project

Fig. 4 is a topographic map of the project area and it's near surroundings.

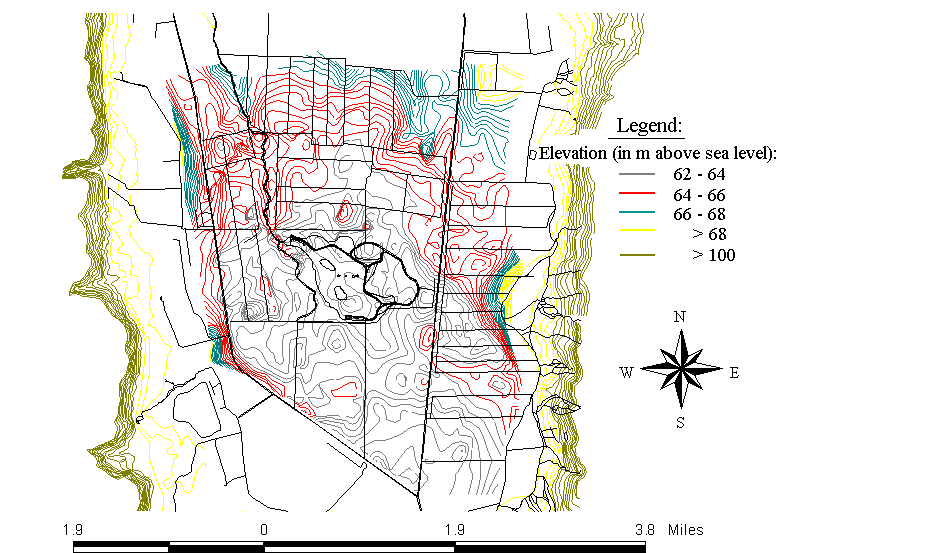
Fig. 4: Topographic map of the Lake Hula project

Fig. 5 shows the locations of the observation wells, and the water quality monitoring stations in the project area.

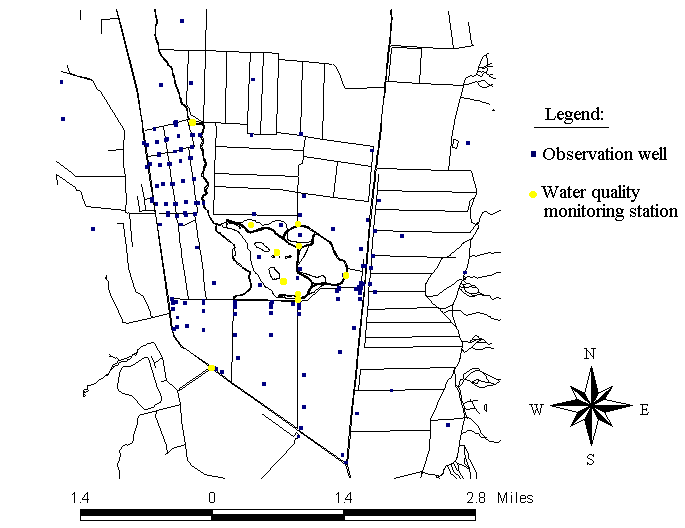
Fig. 5: Location of the observation wells and the water quality monitoring stations

Fig. 6 is a map of the soil types in the Hula valley area emphasizing the peat soil portion.

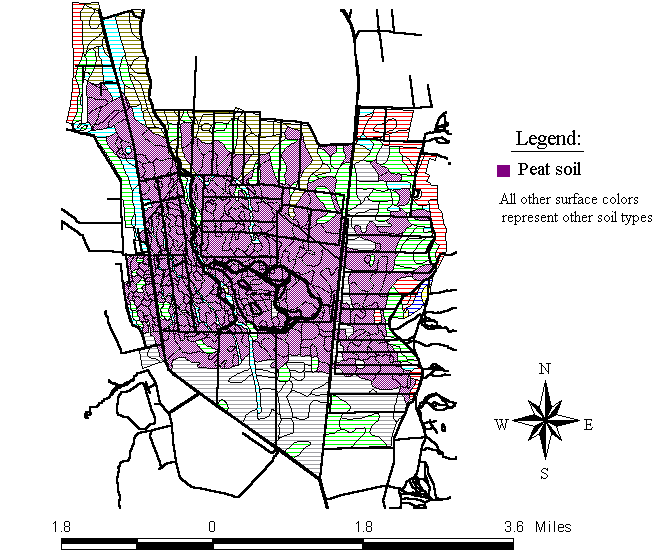
Fig. 6: Soil types in the Lake Hula project area

The Department of Defense Groundwater Modeling System (GMS) is an independent visual groundwater pre and post processing modeling environment linked to groundwater flow and transport models (e.g. MODFLOW, MODPATH) from one side, and capable of importing basic features from GIS data bases like the geometry of feature objects -- from the other.

We are using GMS as our simulation tool for displaying and analyzing the flow regimes in the project area, once the water levels in the drainage canals are determined. We are currently at the process of calibrating the system (i.e. finding the parameters of a given model that are the closest, with respect to a given objective function, to a set of given observations), and so we demonstrate the anticipated simulation outcomes, for steady and unsteady conditions, using arbitrary data. These are shown in Figures 7 and 8, respectively.

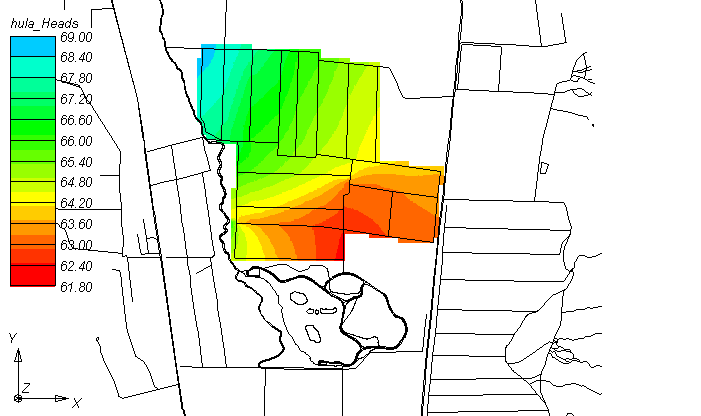
Fig. 7: Example of using GMS to display water levels for steady state conditions for part of the project area

The objective of the LP management model we are implementing is to find the optimal water levels in the drainage canals that results a groundwater table that minimizes the deviations from a specific target domain of groundwater levels in the project area. A management model is required since the water quantities available from the sources are limited (especially in summer), and the water table has to be kept high enough to prevent deterioration of the peat soils from one side, and allow crop growth and cultivation -- from the other.

At each point in time each of the hydraulic structures can be either open (i.e. allowing flow downstream), or closed (i.e. blocking flow downstream). For each such state it is assumed that the domain of water levels within the canals, that in turn form the domain of the boundary conditions, can be defined by a set of linear equations (i.e. it is possible to define a set of linear equations, representing the feasible domain of the water levels within the canals, for a given state of the hydraulic structures).

In formulating the LP management model we use decomposition, justified by the assumption that the feasible domain of the groundwater boundary conditions is only governed by the state of the hydraulic structures. As such, given a state of the hydraulic structures, we define the optimal water table surface as the solution of an "inner" Linear Programming (LP) problem, and the over all problem as a solution of an "outer" integer 0 - 1:

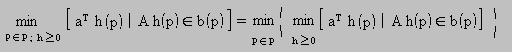
where: P = the set of all the possible hydraulic structure states (indexed p), that is the search domain of the "outer" problem.

The "inner" LP solution defines the optimal boundary conditions and groundwater table for a given p state of the hydraulic structures, under steady state flow conditions. The optimal solution minimizes the head deviations from a desired groundwater head domain, where head deviations at different locations can in general differ. Our rationalization for going directly to steady state conditions is that we assume that the transient stage has little influence on the objective function values, as the damages are based on a long term analysis in which the transient period can be neglected. Nevertheless, each optimal solution can be verified using GMS, thus if our assumption is violated the simulation run will reveal it.

The LP problem constraints include a fully implicit numerical representation of the 2-D flow equations for steady state flow conditions; a set of equations defining the feasible domain of the boundary conditions; and a set of inequalities that define the target domain of the water table.

The LP decision variables are the groundwater levels, the water levels in the drainage canals, and the deviations from the feasible groundwater head domains at each location. The water levels in the canals are the independent decision variables. The LP objective function is the sum of the deviations from the required groundwater head domains, each weighted by a specific damage coefficient.

The overall management problem is to find the hydraulic structure state (i.e. the best p state among the set P) that minimizes the weighted sum of the deviations from the desired water table target domain. The search technique for the "outer" problem depends on its dimension. From a mathematical point of view this domain grows exponentially with the number of hydraulic structures. However, from an engineering point of view this number is significantly reduced as the system is designed to operate under a finite number of states. If this number is not too large than one could simply scan all the states and choose the best one according to the "inner" LP solution. If on the other hand there is a need to use a search technique, than a heuristic discrete optimization technique, such as Simulated Annealing or a Genetic type Algorithm, can be used.

1. Since the hydrology is solved for steady state conditions using the fully implicit scheme, there is no need to specify the initial condition state of the system, which is a great advantage.

2. The global optimum solution of the problem is zero (i.e. no deviations from the groundwater table target).

3. There is always a feasible physical solution to the problem.

4. Since we are using an embedding approach with a numerical representation of the subsurface flow equations (in oppose to embedding an analytical solution), we are much more flexible in accounting for specific properties of the system.

This work is part of a three-year ongoing research project entitled Decision Support System for Arid Land Wetland & Riparian Zones, which is conducted at the University of Arizona. The project is funded by the International Arid Lands Consortium (IALC), whose support is highly acknowledged.

Shaham G. (1995). "The Hula Project-Dynamics of Human Intervention in Nature", in Ecology and Environment, pp. 221-224 (In Hebrew).

Avi Ostfeld is a Research Associate at the Department of Civil Engineering and Engineering Mechanics, The University of Arizona, Tucson, AZ 85721. Tel.: (520) 621-6581; Fax.: (520) 621-2550; E-mail: ostfeld@u.arizona.edu

Kevin E. Lansey is an Associate Professor at the Department of Civil Engineering and Engineering Mechanics, The University of Arizona, Tucson, AZ 85721. Tel.: (520) 621-2512; Fax.: (520) 621-2550; E-mail: lansey@bigdog.engr.arizona.edu

Yigal Salingar is the Director of the GIS group of Keren Kayemet LeIsrael (JNF), P.O.Box 45, K. Hayim 26103, Israel. Tel.: 972-4-8470311; Fax.: 972-4-8470274; E-mail: yigals@kkl.org.il

Thomas Maddock III is a Professor at the Department of Hydrology and Water Resources, The University of Arizona, Tucson, AZ 85721. Tel.: (520) 621-7115; Fax.: (520) 621-1422. E-mail: maddock@ccit.arizona.edu