Constructing Contiguous Area Cartogram uUsing ArcView Avenue

Unlike typical choropleth maps that use graphic symbols to represent quantitative attributes for defined regions, cartograms intentionally distort the boundaries of regions so that the size of the distorted regions is proportional to their attribute. Although an Avenue script for making cartograms is published, it has been rarely used because it has many restrictions and it is time-consuming. Generating a cartogram for a not-so-complex map may require hours of computation, and the resulting cartogram may not be satisfactory. This paper describes an improved algorithm for creating cartograms more efficiently. The new algorithm has been implemented in an Avenue script.

A cartogram is a purposely-distorted thematic map that emphasizes the distribution of a variable by changing the area (or lengths) of objects on the map. Using cartograms, regularities in the spatial distribution of phenomena and interactions among them can be observed more easily. Cartograms are used in geographic investigations, especially for electoral votes or population counts purpose. Cartograms can be classified into two categories, linear and area. Area cartograms use two-dimensional distortions to represent thematic information while linear cartograms express one-dimensional quantities by altering the distance component of maps. Area cartograms may be contiguous or non-contiguous. Contiguous area cartograms distort planimetric maps or produce a desired set of areas while preserving the topology of the original map (Dougenik, 1985). Non-contiguous cartograms are easier to produce than contiguous cartogram because the shared boundaries do not affect the coordinate transformation (Cook 1977). This paper is focusing on contiguous area cartogram, and use cartogram for short.

Traditionally, cartograms have been studied from an academic perspective and the use of them is restricted because they are theoretical difficult to construct. No commercial software including ArcView, the most widely used GIS package, provides tools to construct cartogram. Although an Avenue script for making cartograms is published, it has been rarely used partially because the procedure is time-consuming. Generating a cartogram for a map showing the 50 states of US may require hours of computation. Moreover, it can not handle regions that are divided into multiple polygons. This paper describes an improved method for creating cartograms more efficiently and provides an implemented Avenue program.

Our Avenue program uses the algorithm presented by Dougenik, Chrisman, and Niemeyer (1985). This algorithm uses a model of forces exerted from each polygon centroid, acting on each boundary coordinates in inverse proportion to distance. It can achieve the result iteratively with high accuracy. The concept of the force model can be explained in the formula:

F ij = ( P j - q j) pj / d ij                             (1)

Where: F ij = force exerted by polygon j on vertex i
P j = square root (actual area)/square root (p )
q j = square root (desired area)/square root (p )
d ij = distance from centroid of j to vertex i

Each polygon exerts a force (F ij ) from its centroid to vertices/nodes on all polygon boundaries, including vertices/nodes on the same polygon, which exerts the force. The positive value of the force pushes the vertex away from the centroid while a negative force pulls it toward the centroid. For each boundary node, the force summarized as a vector result from all polygons finally moves the vertex to a new location. From the algorithm, the strength of the force each polygon exerts is determined by selected variable and is proposed to be proportional to the difference between current and desired polygon area. Current area is the actual area of polygon, while the desired area is the distorted area on final cartogram based on selected theme variable. For example, constructing a cartogram for US states based on population, the State of Delaware should exert a strong force because its population weight is larger than its area weight. For state Montana, the situation is opposite.

In each iteration, the sum of the forces from all polygons exerts on every vertex of the map is calculated to displace the vertex. At the end of each iteration, the area of every polygon is recalculated and compared to their "desired area". When the difference between the two areas is smaller than a specified threshold, the program stops.

In order to maintain a good accuracy, the algorithm adopts the concept of distance decay. When a vertex is close to a polygon centroid, the force exerted from that centroid is strong. Further way it diminishes. For example, Ohio’s centroid exerts a much larger force on the boundary vertices/nodes of Kentucky than it has on those of Oregon, which is further away from Ohio. The distance decay function in the algorithm comes with an adjustment, which avoid producing tremendous large force when a node is very close a polygon centroid. When the distance goes to zero, the adjustment produces a zero value.

Although a number of papers devoted to construct cartogram have been published since 1973, Dougenik's algorithm is more practical to implement in ArcView’s environment. The algorithm utilizes coordinate information exclusively and does not depend on inherent topological information to project data from "normal space’ into "distorted space". ArcView match the requirement ideally because the shapefile structure allows no topological inherence. Shapefiles are simple, non-topological formats for storing the geometric location and attribute information of geographic features (Esri, 1994b). In addition, ArcView's object-oriented programming language Avenue provides powerful function to facilitate the customization of graphical user interface (GUI), which allow the user to construct cartograms by simply following the friendly instruction.

Like most algorithms published for constructing cartogram, Dougenik's algorithm requires a large number of iterations. When applied to a map with polygons containing a large number of vertices/nodes, it can be extremely slow (hours to days). For example, the shapefile of the United States (from Esri data) consists of over 13,000 vertices/nodes. It takes over 15 minutes to complete one iterative step even using a high-speed processor computer.

Because the shapefile of ArcView does not store explicit topology, vertices on the shared boundaries are stored twice. As a result, all vertices/nodes on the shared boundaries are calculated twice in every iteration. This considerably slows down the construction procedure.

There are two options to avoid redundant calculation. One is to check topological relationship of all polygons so that the vertices/nodes on shared boundaries will only be computed once. When constructing moderate complex cartogram, this method can save about one third of time. However, since each iteration distorts the map differently, checking the topological relationship before each iteration is necessary.

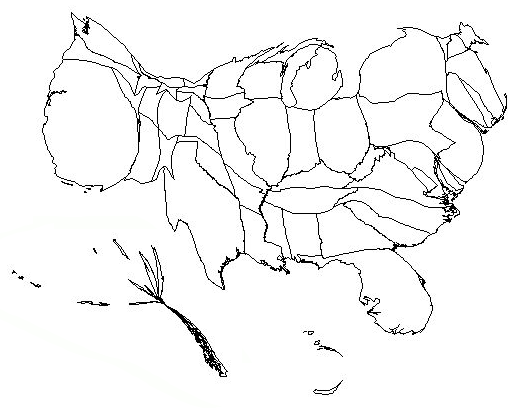
Figure 1: Cartogram of USA based on 1990 population

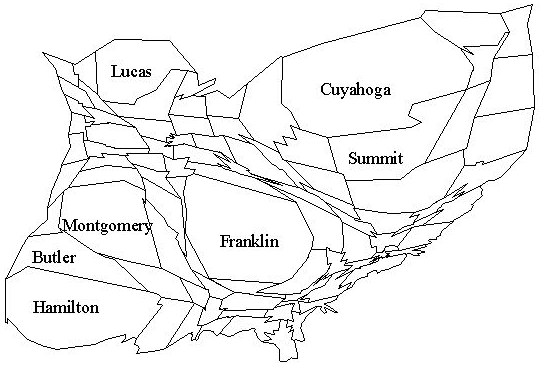
Figure 2: Cartogram of Ohio counties based on 1997 population

Our solution is to split all polygons into polylines topologically and put them into one polyline list. Since each polyline in the list is unique, calculating vertices/nodes from the polyline will not result in doing repeated work. Also, this method allows checking topological relationship only one time, which is done before splitting polygons. Comparing to the first option, another 20 percent of time can be saved. In Avenue, the key is to create an accurate index between the separate polylines and the original polygons. Such index should ensure retrieving polylines to polygons without any mistakes when all the calculation is completed.

polylineList ={polyline 1, polyline 2, polyline i, polyline j, … polyline n}

indexList={{polygon1_Index list}, {{polygon2_Index list}, …{polygonN_Index list}}

polygon1_Index list = { i(polyline i), j (polyline j), k (polyline k) }

As indicated in the above, each polygon and its component polylines are recorded by using a unique index list. For example, according to the index number in Polygon1_Index list, it is possible to find all boundary lines of polygon1 from PolylineList.

Charles Jackel’s Avenue scripts (1997) for cartogram map requires the assumption that all polygons consist of a single ring. This is obviously not the case. 19 of 51 US states are represented by polygons consisting multiple rings, for example, Rhode Island has 3 rings and Alaska has 32 rings. He suggested editing the shapefile prior to converting it into a cartogram by distributing attribute value proportionately to each ring based on its respective area. Obviously, the assumption on the proportional relationship of attribute to area is questionable. Furthermore, redistributing attributes into multi-rings is not a trivial task.

Instead of asking the user to redistribute the attributes to multi-rings, we developed a routine for identifying a centroid for each multi-ring polygon. The first step is to find out the centroid for each ring part using Avenue function "ReturnCentroid". Creating a list containing all rings and using a "for-next" loop can easily get the results. Secondly, average the coordinates of these centroids based on their respective area. Figure 3 shows the final centroid of Michigan State.

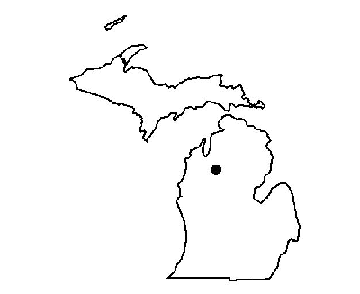
Figure 3: Centroid of Michigan State

The precision of a cartogram can be described in terms of total SizeError mean. SizeError is calculated as the ratio of the polygon’s final area over its "desired" area. In general, a total SizeError mean of less than 10 percent is acceptable for most users. Fewer iterative steps result in larger total SizeError mean. The more iterations, the less total SizeError mean and the more precise cartogram.

The number of iteration needed to produce a satisfied cartogram varies with conditions of the data and polygon being distorted. For example, 24 iterations are required to construct a cartogram for a US map based on population with total size error mean less than 10 percent, while producing a similar map for Ohio counties need only 10 iterations. It should be noted that the user does not know how much iteration they really need. For some instance, user may not be satisfied with the result even after a large number of iterations. They may want to continue with some extra iterations. Therefore, keeping the current result and allowing the program to continue without restarting from the very beginning is of great importance. In the Avenue scripts, an "if " statement provides such option. If the user wants to obtain a more accurate map, the calculation will continue for extra iterations based on the user’s input. By default, the script stops when the total SizeError mean is less than 10%, even if the number of iterations executed is less than what the user specified. This percentage is adjustable.

Figure 4: Iteration number control interface

Generalizing polygons before constructing them into cartogram can considerably speed up the calculation. There is an Avenue script for generalizing polygon boundaries. However, it destroys the original structure of the shapefile, and causes the cartogram algorithm to produce sliver polygons.

In our Avenue program, since polygons have been split into unique polylines with corespondent index list based on their topologic relationship, it is feasible to do generalization without corrupting the polygons.

Figure 5: Option for generalizing polygon

For maps with panhandle polygon, like the shape of State Oklahoma, it is possible to produce crossing borders due to one weakness of the algorithm. However, by inserting one (or more) vertex along the polyline, the program can effectively avoid crossing.

To obtain more correct and precise cartogram, it is the users’ responsibility to ensure their map has proper projection and map units. Non-projection data can not be accepted because the result is not accurate if longitude and latitude is used to calculate polygon area or distance.

Constructing a cartogram has been a formidable task. With the improvement on performance, polygon generalization and others, our script can create cartograms for complex maps in ArcView shapefile format. The eight page long script is not included due to page limits of this publication.

Lin Liu
Assistant Professor, Department of Geography
University of Cincinnati
Cincinnati, OH 45221-0131
Tel: (513) 556-3429
Fax: (513) 556-3370
Email: lin.liu@uc.edu