Environmental
Authors:
Eli Skop and Mario Acquarone
GIS mapping of evapotranspiration in the Vejle Fjord watershed, Denmark
A soil map, land use map and time series of monthly precipitation and potential evapotranspiration were used in a regression model to estimate spatially distributed actual evapotranspiration for the Vejle Fjord watershed. An inverse distance weighting procedure was applied to interpolate monthly precipitation totals between the gauging stations. A comparison of computed catchment average evapotranspiration based on spatially distributed precipitation with computed catchment average evapotranspiration based on catchment average precipitation revealed significant discrepancies. This finding suggests that a spatially variable approach is required to assess catchment average actual evapotranspiration.
Note: all images in this HTML document are linked to the original fullsize images (GIF)
Introduction
In the past many efforts have been put into the question of estimating the mean areal precipitation from point data. Mean areal precipitation, however, do not handle spatial variability. On contrary, when estimating mean areal precipitation from point data, spatially distributed data are lumped together to one average value. The spatial variability of precipitation in our study area is large. The coefficient of variation for the mean annual precipitation for gauging stations for the period 1992-1994 is 0.08. Fortunately, the emergence of powerful GIS in the two most recent decades, has made it easier to handle spatial data and treat spatial variability explicitly. One of the many features of GIS is spatial interpolation. In this study GIS is used to interpolate monthly precipitation totals between gauging stations, which are then merged with land.use maps to produce regional estimates of actual evapotranspiration.
Study area
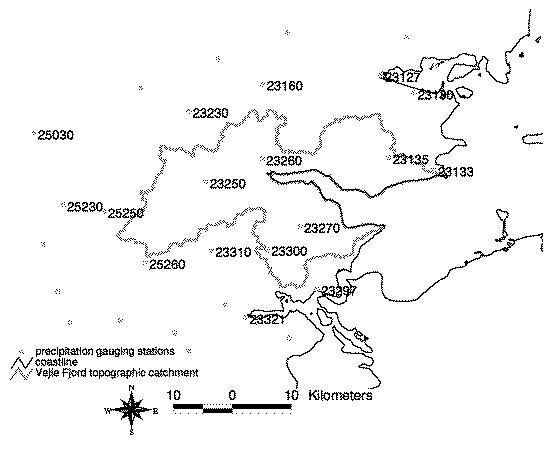
The Vejle Fjord watershed located in the eastern part of Jutland, Denmark, is our study area. The watershed area is 736 km2 and the land-use is predominantly agricultural. Its soils vary from coarse sands to loams. Three landscape elements predominate in the watershed. Its eastern part is mainly younger moraine from the Weichselian glaciation period, while its western area is a mix of outwash plains from the Weichselian glaciation period and old morainic deposits from the Saalian glaciation period. Loamy soils predominate in the east (young moraine geology) and sandy soils overlie the western parts of the watershed (underlain by old moraine and outwash plains). The mean annual potential evapotranspiration is 554 mm and the mean monthly temperature varies from -0.2 oC in February to 15.5 oC in July. Maximum ground elevation is 126 m above sea level. The location of rain gauging stations within and around the watershed is shown in figure 1.
Figure 1. Location of rain gauging stations within and around the Vejle Fjord watershed
Methods
Precipitation data was obtained from the Danish Meteorological Institute [DMI]. Daily precipitation was measured with Hellman raingauges (200 cm2 area ) placed 1.5 m above the ground. Due to errors from wetting losses and aerodynamic effects measured precipitation quantities were corrected to soil surface for moderate shelter conditions using correction factors from Allerup and Madsen (1980) as shown in table 1.
Table 1. Monthly correction factors (%) for standard normals of precipitation due to aerodynamic effects and wetting losses
| station shelter | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec | year |
| unsheltered | 29 | 31 | 31 | 22 | 18 | 17 | 14 | 13 | 16 | 18 | 20 | 25 | 20 |
| moderate shelter | 21 | 22 | 22 | 18 | 15 | 14 | 12 | 11 | 13 | 14 | 16 | 19 | 16 |
| well sheltered | 18 | 19 | 20 | 14 | 12 | 11 | 9 | 9 | 10 | 10 | 12 | 15 | 12 |
Source: Allerup and Madsen (1980).
Mean annual corrected precipitation for gauging stations for the period 1992-1994 is shown in figure 2 and monthly corrected mean precipitation for each year in the period 1992-1994 is shown in figure 3. Monthly corrected mean precipitation is here calculated as a simple (non weighted) arithmetric average of all gauging stations.
Figure 2. Mean annual corrected precipitation for gauging stations for the 1992-1994 period
Figure 3. Corrected monthly arithmetric mean precipitation of gauging stations in 1992-1994
In figure 4 the annual corrected mean precipitation, also calculated as arithmetric averages of all the gauging stations, is shown. Mean annual precipitation for the gauging stations in the period varies from 767.9 mm at station 23130 to 1074.5 at station 23260. Monthly precipitation varies from 0 mm in June 1992 for stations 23250, 23260, and 23300 to 244.5 mm for station 25030 in August 1992. 1994 was the wettest year with 1169.5 mm compared with 870.8 mm which is the corrected average for the 1961-1990 period.
Figure 4. Corrected annual arithmetric mean precipitation of gauging stations in 1992-1994.
We performed the interpolation on monthly totals for each of the three years in the 1992-1994 period. The ArcInfo GRID module inverse distance weighting procedure was applied to interpolate monthly precipitation totals between the gauging stations. The weight assigned to the surrounding gauging stations was chosen as one divided by the distance squared. All gauging stations within a radius of 5 km from the interpolated point were used. In cases where less than four gauging stations were found within 5 km, the search radius was increased until four gauging stations were found. The chosen pixel size was 200 X 200 m. As a result 36 different grids were created, each representing the spatial distribution of total monthly precipitation for each month. Subsequently, grids of monthly totals have been added for each year to give the annual total precipitation for each of the three years.
Mean areal monthly and annual precipitation was calculated for the Vejle Fjord catchment area as total precipitation depth over the area divided by the size of the area. This was done by adding interpolated precipitation values for all 200 X 200 m pixels and dividing by the total area of pixels within the catchment area.
Actual evapotranspiration depends on complex interactions between meteorological conditions, crops and soils. In the present study linear regression models (Clark et al., 1991) based on multiple calculations with the WATCROS (Aslyng and Hansen 1982) model is used. WATCROS is a linear reservoir model that calculates actual evapotranspiration from data on potential evapotranspiration, soil moisture storage, crops and soils. Examples of similar models are the HBV model (Bergstroem, 1973), NAM (Nielsen and Hansen, 1973), the model of Ibrahim and Cordery (1995), the model described by Schumann (1993) and METUL (Krams and Ziverts, 1993). The linear regression models from Clark et al. (1991) are derived using monthly averages of the daily results from the WATCROS model for nine catchments for the period 1961 to 1988. Regression models were developed for each combination of two soil types, four crops and eight months (from March to October). In the remaining months actual evapotranspiration was assumed equal to potential evapotranspiration for all combinations of crops and soil types. The dependent variable in each of the 64 regression models was the monthly sum of daily actual evapotranspiration calculated with WATCROS. The independent variables were precipitation and potential evapotranspiration from the current and the previous month. A detailed description of the regression equations, parameters etc. is given by Clark et al. (1992).
We calculated monthly potential evapotranspiration by adding daily values of calculated potential evapotranspiration using a modified Penman equation (Mikkelsen and Olesen, 1991). The spatial variability in global radiation is much lower than the spatial variability in precipitation, and meteorologic stations measuring global radiation are very sparsely distributed in Denmark. Therefore a single spatially averaged value for the study area was used. Monthly precipitation was obtained by resampling the pixels (200 X 200 m) of monthly total precipitation to pixel sizes of 10,000 X 10,000 m. The resulting tessellation of space is composed of 7x4 pixels and shown in figure 5.
Figure 5. 10,000 X 10,000 m tessellation of space (7x4 pixels) of monthly total precipitation
The agricultural land use was obtained from a previous study by Skop and Schou (1996) who distributed the agricultural farm structure for Vejle County spatially into 50 X 50 m pixels. Skop and Schou (1996) divided all farms into 14 different farm types according to line of production and soil types. In table 2 and 3 a simplified cropping pattern of the farm types is shown by using crop representatives of the various crop groups. Grass is assumed to be representative for roughage, winter wheat for winter grain crops, spring barley for spring grain crops, and fodder beets for root crops. A description of which crops that behave similarly with respect to evapotranspiration is given by Clark, et al.(1992).
Table 2. Cropping pattern of farm types located on sandy soils
| Part-time farms | Small plant production | Large plant production | Small cattle production | Large cattle production | Small pig production | Large pig production | |
| Grass % |
21 | 14 | 9 | 59 | 53 | 10 | 9 |
| Winter Wheat % |
15 | 21 | 29 | 5 | 11 | 22 | 28 |
| Spring Barley % |
63 | 57 | 50 | 35 | 34 | 67 | 59 |
| Fodder Beet % |
1 | 8 | 12 | 1 | 2 | 1 | 4 |
Source: Skop and Schou (1996).
Table 3. Cropping pattern of farm types located on loamy soils
| Part-time farms | Small plant production | Large plant production | Small cattle production | Large cattle production | Small pig production | Large pig production | |
| Grass % |
9 | 10 | 8 | 46 | 32 | 7 | 4 |
| Winter Wheat % |
34 | 34 | 41 | 13 | 28 | 47 | 53 |
| Spring Barley % |
52 | 42 | 39 | 37 | 29 | 45 | 33 |
| Fodder Beet % |
5 | 14 | 12 | 4 | 11 | 2 | 5 |
Source: Skop and Schou (1996)
Calculation of the spatial distribution of actual evapotranspiration for agricultural areas was done as follows. For each monthly precipitation total of the 28 pixels, calculations were performed with the regression models for the four most common agricultural crops (grass, winter wheat, spring barley and fodder beet), for two soil types (sand and loam) and for each non winter months for each of the years 1992, 1993, and 1994. In all 5376 calculations were carried out. Subsequently monthly evapotranspiration for each combination of soil and crop type were added for each year to yield 24 grids of annual evapotranspiration for each combination of soil type, crop type, and year. Then eight grids with 50 X 50 metre pixels, each grid with pixels representing the area percentage of one of the eight combinations of crop and soil type were created. Each of these grids with area percentage of the combinations of crop and soil type were multiplied by the grid of annual and monthly evapotranspiration for the corresponding combination of crop and soil type hereby producing three grids of annual and 36 grids of monthly actual evapotranspiration for the agricultural areas.
Approximately 80 per cent of the Vejle Fjord watershed is agricultural. Other land uses include lakes, forestry, urban areas and natural vegetation. In this study lakes are assumed to evaporate at potential rate. Forestry is assumed to evaporate at 10 per cent above the calculated evapotranspiration from grass. Urban areas and natural vegetation are assumed to evaporate at the same rate as grass. The applied evapotranspiration for non agricultural land-uses is taken from Clark, et al. (1992)
The grids of actual evapotranspiration for non agricultural land uses are merged with grids of actual evapotranspiration for agricultural land use to yield grids of total basin evapotranspiration.
In figure 6 the spatial distributions of annual precipitation for 1992, 1993, and 1994 are shown. The distribution pattern is complex, yet there seem to be a general tendency for precipitation to increase from east to west. However, in 1994 and to some degree also in 1993 a local maximum is found north west of the bottom of Vejle Fjord. Minimum and maximum values are pixels with the lowest and highest values, respectively. These values coincide with the lowest and highest precipitation values from the rain gauging stations since the applied interpolator preserve measured values.
Figure 6. Spatial distribution of annual precipitation for 1992, 1993, and 1994.
Results representing the corrected weighted mean, minimum and maximum annual and monthly precipitation is shown in table 4.
Table 4. Area weighted, minimum and maximum total annual and monthly corrected precipitation.
| area weighted total annual precipitation (mm) |
minimum annual precipitation (mm) |
maximum annual precipitation (mm) |
area weighted mean monthly precipitation (mm) | minimum monthly precipitation (mm) |
maximum monthly precipitation (mm) |
|
| 1992 | 906.6 | 807.8 | 1100.3 | 75.5 | 0 (June) | 200.6 (November ) |
| 1993 | 961.9 | 864.4 | 1093.3 | 80.1 | 10.6 (April) | 189.2 (December ) |
| 1994 | 1169.5 | 1014.9 | 1307.2 | 97.4 | 7.5 (July) | 195.3 (September ) |
source: DMI and own calculations
The spatial distribution of annual calculated evapotranspiration is shown in figure 7.
Figure 7. Spatial distribution of annual evapotranspiration
Mean annual evapotranspiration varies from 321 to 516 . Evapotranspiration was lowest in 1992 with a mean value of 340 mm and minimum value of 287 mm. It was highest in 1994 with a mean value of 434 mm and maximum value of 516 mm.
Comparing distributed and catchment average approaches
The previous sections describe how spatially distributed data for soils, land use, and precipitation ar combined in order to produce spatially distributed data for evapotranspiration. For some purposes, however, mean areal estimates are sufficient. A question that arise in such cases is whether mean areal estimates can be derived using a catchment average approach (based on mean areal input parameters) or whether a spatially distributed approach is required. Obviously a catchment average approach requires significantly less resources to carry out. We therefore compared mean areal evapotranspiration calculated by spatially distributed approach with mean areal evapotranspiration based on mean areal input parameters. The spatially distributed approach is described earlier in this paper. In the catchment average approach mean areal precipitation is used. Mean areal precipitation is calculated by adding interpolated precipitation values for all 200 X 200 m pixels and dividing by the total area of pixels within the catchment area.
For each monthly precipitation total, calculations were performed with the regression models for the four crop types, for two soil types and for each non winter months for each of the three years. Then the area percentage of one of the eight combinations of crop and soil type was calculated multiplied by the monthly evapotranspiration for the corresponding combination of crop and soil type hereby producing the monthly actual evapotranspiration for the actual evapotranspiration. The actual evapotranspiration for non agricultural land uses were added actual evapotranspiration for agricultural land use to yield the total basin evapotranspiration. Figure 8 shows a comparison of model calculated mean areal evapotranspiration using a spatially distributed approach and catchment average approach.
Figure 8. Comparison of computed catchment average evapotranspiration based on spatially variable and catchment average precipitation.
Dicrepancies are identidied especially during the summers where model calculated catchment average values are consistently lower that the corresonding values using the spatially variable approach. During summer periods potential evapotranspiration exceeds precipitation and the soil moisture content is therefore lowered. Soil moisture contents control actual evapotranspiration by decreasing it when water become less available. During part of the summer months potential evapotranspiration exceeds catchment average precipitation, and reduces actual evapotranspiration to almost zero. In the spatially variable approach, part of the catchment is relatively well supplied with water and actual evapotranspiration still takes palce in these wet areas. This explains the discrepancies.
Conclusion
The usefulness of GIS for regional hydrologic applications is demonstrated in this work, where soils, land use, and precipitation maps are processed, merged, and analyzed to produce an estimate of catchment distribution of actual evapotranspiration. A comparison of computed catchment average evapotranspiration based on spatially variable precipitation with computed catchment average evapotranspiration based on catchment average precipitation revealed significant discrepancies. This finding suggests that a spatially variable approach is required to assess catchment average actual evapotranspiration.
Acknowledgements
This study has been financed by a grant from the Danish Research Academy and by a grant from the Danish Ministry of Agriculture and Fisheries as part of a research project: Sustainable Strategies in Agriculture. Precipitation data was obtained from the Danish Meteorologic Institute. Permission to use the soil map was granted by the Danish Institute of Plant and Soil Science.
Allerup, P., and Madsen, H., 1980, "Accuracy of point precipitation measurements," Nordic Hydrology, 11, 57-70.
Aslyng, H.C., and Hansen, S., 1982, "Waterbalance and crop production simulation. Model WATCROS for local and regional application," The Royal Veterinary and Agricultural University, Copenhagen.
Bergstroem, S. and Forsman, A. (1973): Development of a conceptual deterministic rainfall-runoff model. Nordic hydrology 4, 147-170.
Clark D.R., Olesen, J.E. Mikkelsen, H.E., Clausen, S.U. and Waagepetersen, J. (1992): Historical trends in precipitation, evapotranspiration and runoff from nine Danish catchments. Tidsskrift for Planteavls Specialserie, nr. S 2177-1992.
Ibrahim, A. B. and Cordery, I. (1995): Estimation of recharge and runoff volumes from ungauged catchments in eastern Australia. Hydrological Sciences -Journal des Scienses Hydrologiques, 40(4)499-515
Krams, M. and Ziverts, A. (1993): Experiments of conceptual mathematical groundwater dynamics and runoff modelling in Latvia. Nordic Hydrology 24(4):243-262.
Mikkelsen, H.E. og Olesen, J.E. (1991): Sammenligning af metoder til bestemmelse af potentiel vandfordampning. Tidskrift for planteavls Specialserie nr 2157, 1991.
Nielsen, S.E. and Hansen E. (1973): Numerical simulation of the rainfall-runoff process on a daily basis. Nordic Hydrology 4, 171-190.
Simeonidis, A. (1984): Precision in estimating mean areal precipitation for small watersheds. UNGI report no. 60. Upsala University.
Skop, E. and J. S. Schou. (1996): Distributing the agricultural farm structure spatially using fram statistics and GIS. In: Aa. Walther-Joergensen and S. Pilegaard (Editors), Integrated Environmental and Economic Analysis in Agriculture. Report no. 89. Danish Institute of Agricultural and Fisheries Economics.
Eli Skop
National Environmental Research Institute
Department of Policy Analysis
P.O. Box 358
DK-4000
Roskilde
Denmark.
Telephone +45 46 30 12 07
E-mail: es@dmu.dk.Mario Acquarone,
National Environmental Research Institute
Department of Policy Analysis
P.O. Box 358
DK-4000
Roskilde
Denmark.
Telephone +45 46 30 12 07
E-mail: ma@dmu.dk.