(paper # 544)
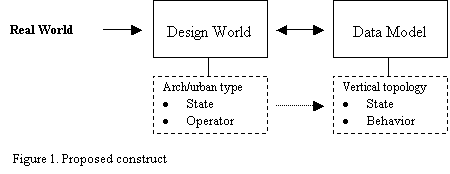
A main advantage of Object component GIS is the ability to more closely match the real world through support of custom data models with specific features. Vertical topology plays a central role in this respect through the incorporation of the features of “state” and “behavior.” This paper presents a theoretical framework and a proposed structure for adopting vertical topology as the basis for building GIS compatible architecture typology. This will result in more precise typological categorization of buildings thus leading to substantive improvements in data base design of urban environments and more informed urban analysis. The argument in the paper is based on vertical topology as developed in ARC/Info V.8, and the theoretical work of William Mitchell on architecture computation and cognition.
INTRODUCTIONIt may be argued that urban environments represent the highest order of complexity in human endeavors. Their complexity results from the wealth of physical elements of which they are composed, as well as the nature of the relation between them. It follows, then, that the discipline of urban planning can benefit from tools and procedures that help improve our understanding, production, and management of organized complexity.
In view of the increasing challenges faced by planner struggling to introduce order and coherence on the seeming confusion and fragmentation of ever expanding cities, the value and significance of such documents as land-use plans, and zoning maps were called into question and criticized as too rigid and limited. As two-dimensional documents, plans have inherent ambiguities of interpretation, particularly in the third dimension. Often, they are concerned with formal simplicity and visual purity, ignoring the processes of organization which are rarely visually simple.
Advances in information technology have helped us understand complex systems. Thus, reducing the need for simplified assumptions, typical of the earlier practices of urban analysis and modeling. This paper examines two such advances and their potential in improving the informating capacity of plans and maps. The first is the notion of the Design World as developed by William Mitchell in his book The Logic of Architecture: Design, Computation, and Cognition. The second is the development of vertical topology in object-component GIS databases models as developed by Esri , Arc/Info V.8.
The proposition put forward here is that the design world is a useful mediator between the real world and the database model. Its value comes from it being a source for the information necessary for the formulation of ‘state ‘ and ‘behavior’ in vertical topology. This is achieved through the interaction of the structure of the design world, characterized by state and design operation, with the domain or discipline specific body of knowledge defined to as architecture and urban typology.

DESIGN WORLD:
Mitchell presents the design world as a conceptual tool to depict possibilities in the larger world. He argues that: ”the potential translation into physical reality may or may not actually take place or have any prospect of taking place; it suffices that such translation is possible in principle.” When a computer-aided design system is used, the data structure and its associated operations establish the design world.
In a computer implementation of a design world, geometric primitives are typically stored as records. Grouping of primitives into shapes might be expressed by providing pointers from primitive records to shape records, or by setting up appropriate tables. Functions and relations of shapes might be expressed explicitly by storing tables in a relational database or implicitly by providing procedures that can be executed to return values of functions or lists of shapes in specific relations. (Mitchell 90)
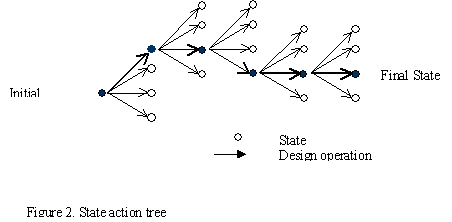
The state action tree metaphor:
Design worlds unfold through the interaction of states and design operations. A design operation changes a design world from one state to another. “The set of all states reachable by performing design operations, then, becomes the universe of possibilities that a designer explores in search of design solutions.” This universe may be pictured as a state-action tree in which the root is the initial state, internal nodes are possible states, and branches are available design operations.
State:
In the simplest case, state is a binary variable integral to the definition of graphic or geometric primitives in a design world. In a computer-aided design system, a state is a particular binding of values to the variables in the data structure. (Mitchell 90)
Design Operators:
A design operator is a tool for manipulating shapes in a design world. More formally, an operator is a function that evaluates to a new state of the design world. In a computer-aided design system, the operators are programs that manipulate the data structure.
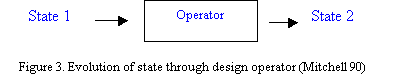
The meaning of a design operation in its entailment – the set of facts that become true as a result of it and the set of facts that become false. If we can specify an initial state of a design world, plus a set of operators characterized in this way, we have established the state-action tree for the world. Its branches are all the branches that can be constructed by recursive application of the set of operators to the initial state.
In principle, state-action trees usually branch luxuriantly and rapidly become enormous. However, they are always limited to the territory staked out by some set of assumptions about shape primitives and their possible properties and relationships (Mitchell 90). For the purpose of the argument presented in this paper, architecture typology is regarded as the source for such assumptions.
Data modeling describes the process of abstracting and representing the real world in a computer. GIS data models are concerned with representing geographic objects and their relationships digitally. A feature of central importance in this respect is topology. Topology is a mathematical procedure for explicitly defining the spatial relationship between features. It is the highest level of generalization at which geographic features can be stored. Creating strong topological relationships has a number of advantages. Data is stored more efficiently and processed faster, and in larger sets. When topological relationships exist, it becomes possible to perform analytical functions, such as modeling.
Over the last 30 years several different data models have been tried in GIS with varying degrees of success. In the database-oriented GIS the geo-relational model has been widely and successfully employed for over a decade. In this model the geometry and topology of geographic features are stored in files with attributes in a database management system (DBMS). The link between the files and the database is managed by the GIS software. This model is geometry-centric, modeling the world as a collection of geometric features (such as points, lines, and polygons), with operations on geometry encoded as separate procedures (AML scripts). The geo-relational data model has served GIS users well for many years because of its flexibility, extendibility, and good performance. However, this approach has limitations for modeling the richness of geographic objects. Furthermore, it cannot be easily extended to support user-or domain-specific features. (Maguire 98)
To address these problems, object-based data models were introduced. The key reasons for moving to an object-component model include having a GIS that more closely matches the real world; more scope for extension and customization, in particular support for custom data models with specific features. These allow the state and behavior of objects to be modeled in an integrated way in a GIS. The state of an object can be thought of as the properties or attribute data of an object. The behavior is the methods and operations that can be performed on an object.
The key issue to be considered here is that the object-oriented data model provides a means to encapsulate behavior with feature data and allows developers to create custom objects relevant to particular domains and work with them as objects rather than simple geometric features. This is referred to as vertical topology. This new breed revolutionized GIS in several ways. They made systems easier to use: the software is now able to deal with user-oriented concepts like buildings and one-way streets, and not system-oriented concepts like points, lines, and polygons, thus setting new standards for user interaction, extendibility, openness, and data modeling (Maguire. 98).
TYPE IN ARHITECTURE:
Architecture, we mean here the world of objects created by architecture, is not only described by types, it is also produced through them. If this notion can be accepted, it can be understood why and how the architect identifies his work with a precise type. Thus, the design process is a way of bringing the elements of a typology- the idea of a formal structure- into the precise state that characterizes the single work of architecture.
From the point of view of typology, a work of architecture can be seen as belonging to a class of repeated objects, characterized, like a class of tools or instruments, by some general attributes. Type, in this sense, could be defined as the “inner formal structure” of a building or series of buildings. In reference to the Gestalt this could be understood as trying to characterize form in terms of a deeper abstract geometry. It can thus be considered equivalent to the notion of “state” in GIS topology describing the properties or attribute data of the architectural type. Furthermore, precise types resulting from technical definitions are essential for their incorporation in computer databases.
In addressing the notion of type, Mitchell raises two significant questions. First, what classes do we want to recognize in conceptualizations of buildings? Second, what properties do we want design/building elements to inherit by virtue of class membership? In response, he proposes two concepts of type: precise types, and fuzzy types.
Precise Type:
This concept of type is characterized by precise and complete formulation. A further distinction in this concept of type is that between essential and accidental properties of an object. Essential properties are those that it shares with others of its type, and are necessary conditions. Accidental properties may vary from instance to instance within a type. If a necessary condition is not satisfied, then an object cannot be an instance of the type. But satisfaction of a necessary condition might not guarantee that it is an instance, since other necessary conditions might remain unsatisfied.
Fuzzy Type:
Attempts to produce precise and rigorous definitions of types typically yield lengthy, cumbersome lists of exceptions. So, another way to handle the above problem is to abandon insistence on necessary features and sharp precise type definitions, and develop instead an approach based on family resemblance. On this view, type schemata and boundaries of types are fuzzily defined.
In this early work Mitchell resorted to frame formalism as introduced by Minsky (1975), which provides a particularly general and flexible way to take account of these complexities in the formulation of type definitions. The frame consists of slots and slot fillers. A slot may be filled or unfilled. The filler of a slot can be an actual value, a default value, a procedure for finding a value, or another frame. An actual value is one we know to be true, while a default value is one that we assume to be true until we learn otherwise. Thus, default values encode expectations that can be adjusted, if necessary in specific contexts. (Mitchell. 90)
Reading and Interpreting Drawings:
Organization of knowledge within the framework of some system of types enables us to read architectural drawings, as well as other depictions, constructed within design worlds. We do so through a two-step process: shape recognition, then interpretation.
Shape recognition:
1. Discrete shapes: where shapes are discrete, recognition is relatively straightforward. We can apply recognition rules to label the shape instances appropriately.
2. Complex shapes: More often, though, a drawing presents a complex scene, and the task becomes one of sub-shape recognition-breaking the scene down into parts and searching through the collection of parts to find those that qualify as instances of the shape type that interest us. This too, is straightforward if we treat shapes, as most CAD systems do, as sets of discrete, indivisible primitives, such as vectors and arcs.
Interpretation:
Two dimensional design worlds have inherent ambiguities of interpretation. The famous rabbit/duck drawing clearly illustrates such ambiguity.
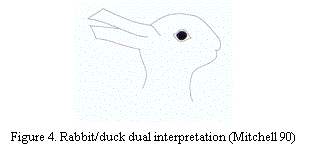
The interaction of domain knowledge in interpolation of a depiction reduces such ambiguity. The assumption presented in this paper is that architecture typology is one kind of domain knowledge, which is useful for informed interpretation of map and plans in the context of urban modeling and analysis.
The reading of drawings can be established in two different ways. If the drawing was built up from graphic primitives and abstract shape types, then recognition rules must be applied to produce an interpretation as an arrangement of architectural vocabulary elements in the construction world. But, if the drawing was built up by instantiating labeled objects, then the interpretation of shapes as vocabulary elements in the construction world is given a priori. (Mitchell 90)
BUILDING INFORMATICS:
In the introduction of the paper we argued that the complexity of urban environment results from the wealth of physical elements, as well as the relations between them. In this section examples are presented to illustrate the above discussed proposition. The first category examines topology building based on form driven architectural typology. The second examines topology based on operation/procedure driven architecture typology.
As discussed earlier in this paper, architectural types are defined by unique formal characteristics embodied in the inner formal structure of the building or series of buildings which belong to the type. The architectural discourse in the realm of history and theory is rich with numerous studies and theses on the origin of type and the classification of typology. These provide an invaluable resource for the articulation of the notion of state in the design world. This, in turn, is necessary for the building of state in vertical topology.
In the following pages the architecture types Mosque and churches will be discussed as two examples of form based typology.
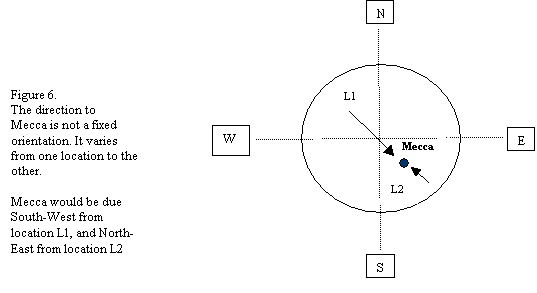
1.1Mosques are typically rectangular in plan with the distinct feature of one of the sides of the rectangle facing to the direction of Mecca. Since this orientation is unique to mosques, it usually renders them easily recognizable in any urban fabric.
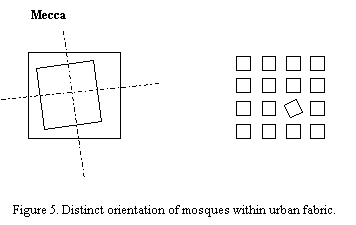
Thus, orientation towards Mecca becomes an essential characteristic of this precise type. Orientation could be incorporated into the system in one of two ways. In the form of a table containing specifying accurate orientation coordinates for major cities. The table could be pulled out from a menu and the relevant city selected. Alternatively, a procedure could be initiated which calculates the orientation once the relevant coordinates of the specific city are entered based on the shortest path to Mecca from the site/city under consideration.
Size may be treated as an accidental characteristic which helps further distinguish sub-types of the architecture type mosque. By calculating the area of the prayer spaces, and then dividing that over the prayer module per person [average of 0.8 sq.m.], the capacity of the mosque can be calculated. A mosque with a capacity of up to 40 persons, it is categorized as a “musalla. The mosque with the largest capacity in a given distinct urban sector, say municipality or suburb, is considered as the congregational mosque, or Masjidi jami’e. As such, not only would the GIS system be able to identify mosques through reading a map of a given urban context, but it could also categorize them in sub-types based on size/capacity.( Abu H. 85)
1.2 Churches are another architecture type characterized by essential formal qualities that can be depicted in plans. It is conventional that plans of churches are cross-form in shape. While the cross-form is essential, a variety of plan interpretations do exist.

Confusion may potentially arise between the centralized plan shape and the cross-form plan shape. To avoid that, more accurate type definition of the cross-form plan is needed. This is achieved by incorporating the following formal qualities: a centralized zone, extensions in east-west direction, as well as the presence of the altar at the east end.


Operation driven typology (relations):
Operation driven typology (relations):In this approach the driver of the typology is the set of rules and operations, rather than the form. A good example to illustrate the point are zoning ordinance and building laws. Often, analysis of urban fabric at the macro level provides limited insight on the impact of zoning regulations and building laws in the shaping of such fabric. The most informative approach is to conduct such analysis on the individual lot scale. Typology empowers approach.
In principle, laws and regulations define fuzzy types. These generate numerous precise instances through the interaction of the laws and the regulations, set as default values, with the particularities of the each lot. The example detailed below helps illustrate the point. =
Developed lot
Building
Land
Figure 10. Components of a developed lot.
A basic assumption in this respect is that a developed urban lot, can be defined as an object composed of a piece of land and a building which sits on this piece of land. The relation between the building and the land is defined by zoning ordinances, and the building law. The characteristic qualities of the building will result from the application of a set of laws/ procedures. These are:
The building footprint is a function of mandatory setbacks, or the specified surface exploitation factor and often is a function of both. The area delineated by the setbacks is always equal to, or larger than the maximum building footprint.

The building characteristics are produced as follows:
Maximum building foot print = area of land * S.E.F.
Total built-up area = area of land * F.A.R.
Number of floors in the building = total built-up area / building footprint
Building height = total number of floors * default floor height.
Default floor height is estimated by adding minimum allowed floor to ceiling height and typical slab thickness based on construction conventions.
To illustrate the point, the following example is presented.
Assume we have a lot with the following characteristics:
It follows then the building on the lot will have the following characteristics:
In the second case, let us assume that the setbacks do not actually coincide with the S.E.F. so that the building foot print is potentially a variable. And let us also assume that zoning regulations fix the building the height at a maximum of 21 meters. Then we can use the above set of operations to determine the maximum floor area and the building envelope. This can be achieved as follows:
Maximum number of floors = Max. allowable height / typical floor height
= 21 meters / 3.25 meters = 6.46 floor (6 floors)
Floor area = total Built up area / number of floors
= 3000 Sq. m. / 6 = 500 sq.m.
From the above examples we learn that operational types are fuzzy in nature due to the potential difference between default values assumed, in view of building codes and zoning regulations, and actual values of every case, which are often different correct implementations of the same set of rules.
We also learn that by incorporating object-components, such as those discussed above, it becomes possible to reduce the ambiguities inherent in plans and maps, rendering them more informative of the architecture/urban context they represent.
By building such relations in the database we are able to extrapolate the total built-up areas, building heights, and number of floors without having to resort to site surveys.
CONCLUSION:
REFERENCES:
Abu.H Imamudin et. al. “Community Mosque – A Symbol of Society.” Regionalism in Architecture. Publishd for the Aga Khan award for Architecture by Concept Media Pte Ltd, Singapore, 1985, pp60-69.
Ching, Francis, Architecture: Form, Space, and Order. Van Nostrand Reinhold Publishers, New York, 1979.
Frankl, Paul. Principles of Architectural History: The Four Phases of Architecture Style, 1420-1900. MIT Press, Cambridge MA, 1968.
Maguire, David J., “ARC/INFO Version 8: Object-component GIS.” ARC News, Vol. 20, No.4., 1998/99, Environmental Systems Research Institute, Inc. Redlands, CA, pp.1-2-5.
Mitchell, William J., The Logic of Architecture: Design , Computation, and Cognition. MIT Press, Cambridge, MA, 1990
Tarek Kazzaz
Associate Professor
Department of Architecture and Design
American University of Beirut
Beirut, Lebanon
Email: kazzaz@aub.edu.lb