Model-Oriented Generalization Rules
Hae-Kyong Kang1,
Soon-Hee Do1,
Ki-Joune Li1, and Byung-Nam Choi2
1
Department of Geographic Information Systems,
Pusan National University.
{hkkang,shdo}@quantos.cs.pusan.ac.kr
lik@hyowon.cc.pusan.ac.kr
2
Korea Research Institute for Human Settlements.
bnchoe@krihs-web.krihs.re.kr
This paper presents a set of rules for
deriving a new database from a preexisting one in GIS. If we apply map
generalization operators in ArcInfo to the database, it results in evolutions
of a data model. We need to control these evolutions for a successful
derivation of a new database. In order to control evolutions, we first
investigate effects of generalization operators upon data model. Specially, we
classify the effects of six generalization operators - preselection, elimination, collapse,
simplification, geo-aggregation, classification- upon a data model. And we
propose a set of model-oriented generalization rules for the effects.
Database derivation is a useful way in building a new database in GIS. It is one of four application fields mentioned in [Lag94] which need generalization facilities. Generalization in GIS transforms data into an adequate one to be represented at a smaller scale [McMaster92, Esri96, Dettori98, John99]. It means that generalization derives new data through transformation of the spatial and non-spatial properties of a feature.
A feature contains four elements including geometry, non-spatial properties, topological relations and non-topological relations[Tang96]. These elements are changed through generalization. First, generalization operators changes the geometry of a feature where it generates scale-dependent data. This generalization has been called map generalization or cartographic generalization since it concerns only geometric changes. Secondly when a geometry is changed, topological relations, non-topological relations or both can be changed as well. The generalization must preserve consistency of topological relationships[Dettori96, Dettori98]. And it may create, delete or derive features and non-topological relationships[Peng96, Richard94, John96]. When a non-spatial property is changed, it causes a set of changes of geometry, topological relationships or non-topological relationships can be changed. These generalizations are called model-oriented generalization, since it concerns changes of data model in GIS databases.
In this paper, we propose a set of rules for changing topological relations, non-topological relations, spatial properties and non-spatial properties in model-oriented generalization. We first give a list of ten components of data model which are to be considered during the generalization[Tang96, Rumbaugh91]. They serve as a basic concept for model-oriented generalization in the rest of this paper.
It is for a framework of a data model for model-oriented generalization. Then we select six generalization operators through comparison of previous studies [Beard91, Ruas93, Lee93, Lag94, Dettori96, Esri96, John96, Peng96]. We investigate effects of these operators upon a data model. And we propose a set of model-oriented generalization rules for deriving a consistent database.
This paper is organized as follows. In section 2, we investigate related studies. In the next section, we give descriptions on the framework of data model change for model oriented generalization. Then we propose a set of model-oriented generalization rules using object-orient concept in section 4. We present an example in section 5. Finally, section 6 concludes this paper.
A need of generalization in GIS environments has been widely recognized. [Lag94] cites four application fields of generalization that is data visualization, data integration, derivation of databases and data analysis. In data visualization, the generalization selects adequate data which are dependent upon a scale. This generalization has been called map generalization and many studies have been proposed since the mid of 1970¡¯s[McMaster92a]. In data integration, data analysis and derivation of data, the generalization integrates with multi-scale databases into a new database and it requires more complicated procedures than the map generalization contains a number of issues listed in table 1.
Table1. Issues in generalization
| Issue | Related study |
| - data selection - creation of new information (etc. class, relation) - data derivation from an implicit one of a source database - updating derived data - changing topology - semantic/schematic conflict - maintenance of consistency - maintenance of propagation |
- Model-oriented generalization operators [Beard91, John96, Peng96, Dettori96] - Multi-scale data model [Rigaux94, Rigaux95, Barne-tt96,Barbara95] - Rule to derive data [Richard92,Sester98] - Object abstraction [John96, Richard94] - Linking or translation among objects [Miller93, Atzeni95, Devog98, Sester98 - Integration data model [Atzeni97, Bennett97 ] - Schema analysis methodology [Nyerges89, Castano99] |
From database point of view, a model-oriented generalization includes a process to derive new data model from source data model. If a data model consists of classes, relations and constraints, generalization contains a process to derive classes, relations and constraints from source ones.
Previous studies have concentrated on derivation of new classes[Beard91, John96, Peng96, Dettori96, Sester98]. To create a new class, they used an object abstraction and generalization operators. We summarize the effects of the operators upon a class(Table2).
Table2. Category of an effect
|
Type of effect |
Beard91 | Dettori96 | John96 | Peng96 |
| spatial dimension | Coarsen Collapse |
Simplification Symbolisation |
(none) | Collapse |
| number of an object (or instance) | Omit Select |
Selection | Selection | Deletion Aggregation Simplification Homogenization |
| number of an attribute and a feature | Classify Combine |
(none) | (none) | Universalization |
| number of a class | (none) | Aggregation | Generalization Aggregation |
Universalization Reclassification |
However these researches have concentrated on the change of a class itself without considering its relationships with other classes or constraints. In order to derive a data model with rich semantic, the model-oriented generalization must include derivations of relationships and constraints in addition to the class itself. In this paper, we will investigate derivation rules concerning them for model-oriented generalization.
A feature is an object that represents phenomenon in a real world. A feature has been defined as a primitive unit of GIS databases such as DLG-F(USGS), DNF(Ordnance Survey in UK) and core data of the national framework GIS database (Republic of Korea).
[Tang96] defined that a feature contains positional information(geometry), non-spatial properties, topological and non-topological relations. And relations among features includes abstractions like generalization, aggregation in feature-based GIS.
3.1 Components of feature-based data model(GIS data model)
Based on [Rumbaugh91, Tang96], we describe ten elements and notations of feature-based data model as shown by Figures 2. In order to completely define schema and semantics of a class C, related class of C might be needed such as super class Csp, component class Ccl and domain class Cspatial. If a class C is migrated to a new database, those classes and relations must be migrated. Table 3 describes definition of each component.
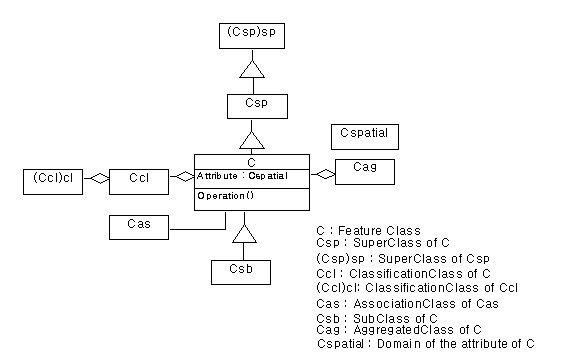
Figure2. A framework of feature-based data model
Table 3. Ten components of feature-based data model
| Component | Description |
| Feature | A feature is an object in database. It has attributes and operations. They represent spatial and non-spatial properties of feature. |
| Feature class | A feature class is a group of similar features. A feature class has its own topological relationships. For example, a feature class Building has face-edge, face-node and edge-node relations. A feature class Road has edge-node relation. |
| Spatial object class | It represents a spatial property of a feature such as location. |
| Domain of feature attribute(Attribute:Cspatial) | It is a class or data type which may be provided as a built-in type or user define type. But we do not treat the built-in type for the domain of feature attribute in this paper. |
| Generalization | Generalization is a TYPE-OF relationship between a class C and generalized one Csp super class of C. |
| Specialization | Specialization is a IS-A relationship between feature class C and its sub class Csb. |
| Classification | Classification is a CONSISTS-OF relationship between class C and component one Ccl. |
| Aggregation | Aggregation is a PART-OF relationship between class C and combined one Cag. |
| Association | This is a REFERENCE relationship except generalization, specialization, aggregation and classification between feature classes. |
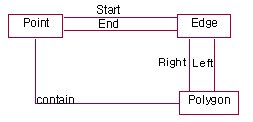
| Topological relation | Topological relations between spatial objects are those that are preserved under ¡®rubber-sheet¡¯ transformations, which continuously deform the underlying space [Worboys97]. |
We use the topology model used in ArcInfo, which supports three topological relationships that are polygon-edge, polygon-point and edge-point relationships as illustrated by Figure 4.
We select six generalization operators from [Esri96] : preselection, elimination, simplification, collapse, aggregation, classification. These operators defined in similar ways in [beard91, Lee93, John96, Peng96, Dettori96, Ruas93, Lag94](table2). For example, preselection[Esri96], select[Beard91] and selection[Dettori96, John96, Peng96] indicate the same operator.
It selects a subset of feature classes from a source database for an inclusion in a new database. Feature selection is dependent on the purpose of given application.
It selectively deletes features that do not satisfy the conditions given by application.
It removes unnecessary details from features without destroying its essential shape.
It reduces a spatial dimension of a feature. For example, if scale is reduced, polygon features must be symbolized as points or lines.
It combines features in a close proximity of adjacent features into a new polygon feature.
It merges adjacent features which have the same attribute into a new higher-level feature.
If the six generalization operators are applied to feature-based database, they result in changes of geometry, topological and non-spatial relationships and non-spatial data. These changes can be divided into three groups(Table3).
Table4. Effects of generalization operators| Group | Type of an effect | Generalization operator |
| 1 | Determine existence of a feature | |
| 2 | Transform spatial properties of a feature(spatial transformation) | Simplification, Collapse |
| 3 | Re-classify features into new feature.(attribute transformation) | Geo-Aggregation, Classification |
An object-oriented concept serves a basic concept in order to completely define semantics and schema of a feature. Using this concept such as classification and generalization relation, we can decide an existence of related feature to source one, which is selected by generalization operators in group 1. To successful decision, we propose the following rules.
[Rule1] If a class C is derived into a class Cgen of target database, its super class Csp must be derived into target one as well.
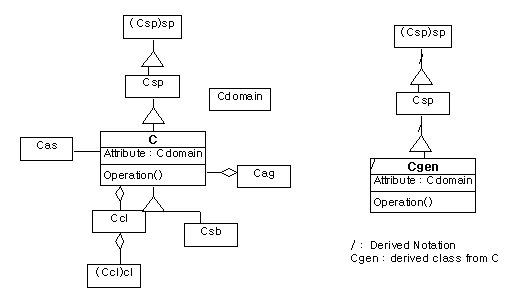
a. a source model b. a target model(the result of rule 1)
Figure5. Model-oriented generalization rule1
[Rule2] If a class C is derived into a class Cgen of target database, its component class Csb must be derived as well.
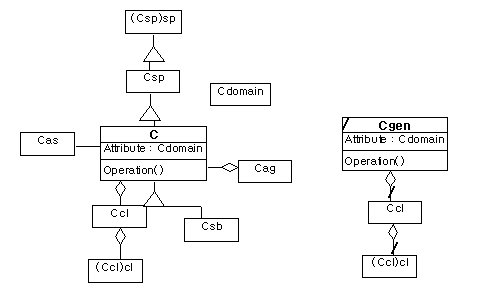
a. a source model b. a target model(the result of rule 2)
Figure6. Model-oriented generalization rule2
[Rule 3] If a class C is derived into a class Cgen of target database, its domain class Cdomain must be derived as well.
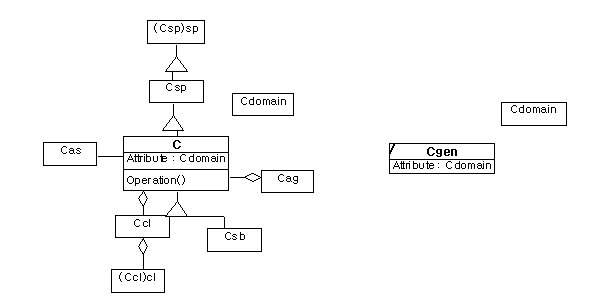
a. a source model b. a target model(the result of rule 3)
Figure7. Model-oriented generalization rule3
[Rule4] If a feature fof a class C is eliminated, its referencing feature must be removed.
In order to successfully derive a new data using generalization operators in group2, we must preserve topological relationships of features. The following rules support the preservation.
[Rule5] When the geometry of a feature is changed, topological relationships and topological consistency between spatial objects must be preserved.
[Rule6] If the spatial dimension of a feature is changed, new topological relationships for a new dimension are to be created.
The operators in group 3 create a new feature class. In order to derive new feature classes, we propose a set of rules.
[Rule7] If a new feature class is created, new topological relationships must be created for the new one.
[Rule8] The numeric attributes of a new feature class can be derived from the original ones by set-functions such as sum(), max(), min() or average().
[Rule9] If a feature class Cgen is created from C, an aggregation relationship is to be created between C gen and C.
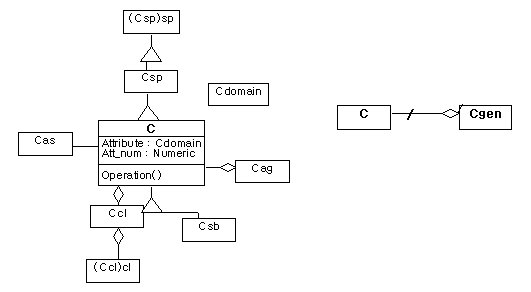
a. a source model b. a target model(the result of rule 3)
Figure8 Model-oriented generalization rule9
We proposed nine rules for model-oriented generalization in the previous section. These rules are used with generalization operators. This section describes that the rules are applied to data model with six generalization operators that we described in this section.
If a feature class C is selected in a source data model, rule1 derives the generalization hierarchy of C that contains Csp,(Csp)sp and generalization relation between them. Rule 2 derives the classification hierarchy of C that contains a class (Ccl)cl, Ccl and classification relation between them. And rule 3 derived domain of C that is Cdomain. As a result, six classes and relations among them are derived by preselection and rule 1, 2 and 3(figure9. b).
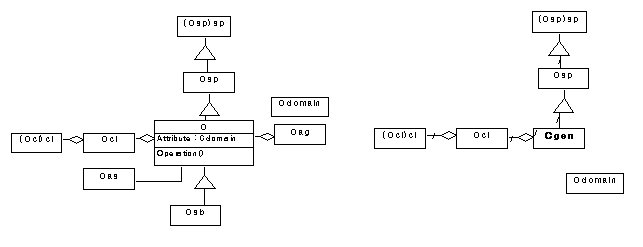
a. a source model b. a target model(the result of rule 3)
Figure 9. Preselection and rule1, 2 and 3.
*Elimination and RulesThe elimination reduces the number of a feature. In this case, we must break its referencing feature to preserve consistency of database. The operator is applied with rule 4.
Simplification changes the geometry of a feature and consequently the topology model is changed as well. Rule 5 preserve topological relationships among spatial object classes from the propagation.
Collapse reduces the spatial dimension of feature. As a result, a new feature class, which has lower spatial dimension, is created. The new feature class derives non-spatial attributes of a source feature. Rule 3 loads the domain of a source feature into a target data model. Rule 6 creates a new topological relationships of the feature class.
A classification creates a new feature class Cgen from a class C in a source model(figure10 a.) At this time a new aggregation relationship must be created between Cgen and C.Therefore the classification is related to rule 3, 7, 8 and 9.
Rule 3 derives the domain of C. Rule7 creates a new topological relationships for Cgen. Rule 8 creates a new attribute SetAtt of Cgen from the attribute Att_num of C. Rule 9 create a new aggregation relationship between C and Cgen.
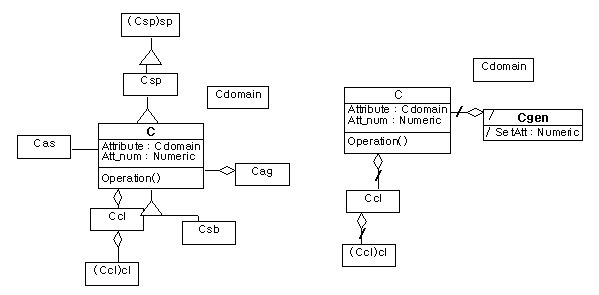
a. a source model b. a target model(the result of rule 3)
Figure 10. Classification and rules
A geo-aggregation combines features in close proximity of adjacent features into a new feature. Although its geometric derivation is different from classification, the classes of data model is identical to those in classification. The operator creates a new feature class. Rule7 creates new topological relationships for the new feature class. Rule 8 creates a new attribute. Rule 9 creates a new aggregation relationship.
We developed a model-oriented generalization tool supporting the a set of rules we proposed and six generalization operators on ArcInfo desktop 8.0.2 using ArcObjects and Visual Basic Application. We show important functions of our system with an example.
This example describes the process of deriving a new smaller scale database from 1:1000 database for an application. To derive a new database, our application first support a user interface to analyze the data model of a source database. Then it requests a set of conditions which a new database satisfies with. And it applies generalization operators and a set of rules to the data model.
We use a part of the landuse database that is built by the Korea Research Institute for Human Settlements. Figure 11 shows a source data model for this example.
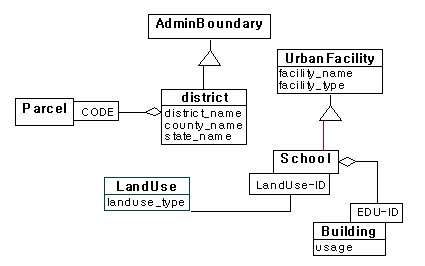
Figure 11. A source data model
A new database must satisfy the following conditions.
Condition1 A target database must include County, State and School. To createState, we use District and state_name of District.
Condition2 If the value of state_name of a District feature is suwon, the District feature is loaded into a target database.
Condition3 We set the scale of a target database for 1:5000. Simplify the resolution of a District feature adequately to represent at1:5000 scale. A proper tolerance to transform 1:1000 to 1:5000 is given 100.
We will use preselection operator and classification operator for condition1, elimination operator for condition 2, simplification for condition 3. The results of generalization can be changed by operator sequence. But we do not consider the sequence in this paper. We will apply operators in preselection, elimination, classification, simplification order.
First, the application display a user interface to analyze source data model. Figure 12 shows the interface for data model analysis. It supports that a user sets relations between classes.
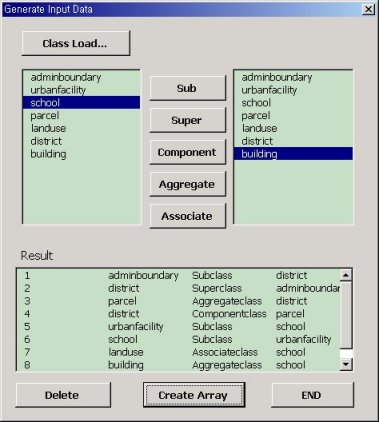
Figure12. Analysis of source data model
In this section, we show examples that apply a set of rules to generalization operators for our application.
From the condition 1, preselection selects two classes that are District and School. Preselection is applied with Rule 1, 2 and 3 to a data model. Rule 1 derives the generalization hierarchies of District and School. As a result, Boundary and <>UrbanFacility are selected. Rule 2 derives the classification hierarchies of District and School. Parcel and Building are selected. Rule 3 derives domain for a derived class. In this example, there is no proper class.
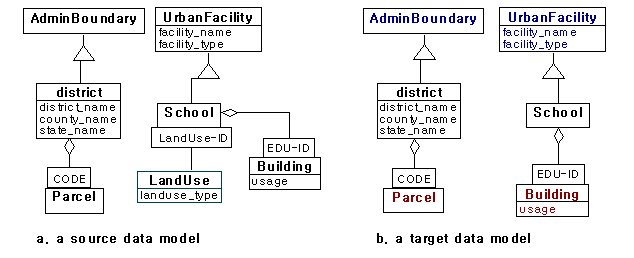
Figure13. Example (preselection and rules)
The following figure shows that if School is selected, UrbanFacility and Building are selected according to rule1 and 2.
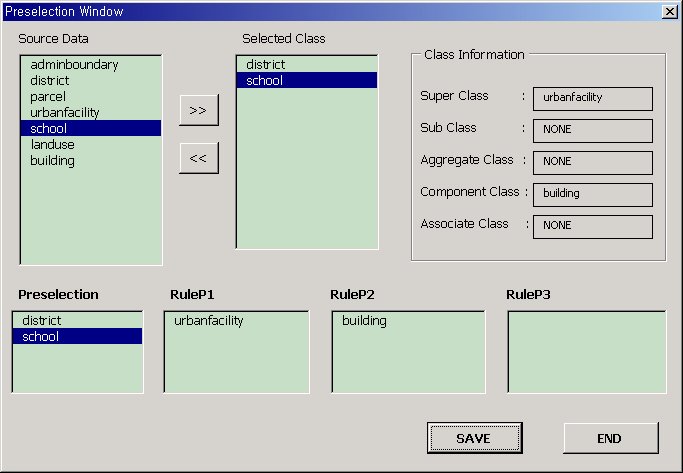
Figure 14. School example of preselection and rules
Elimination selects district features, which satisfy District. state_name = suwon, to delete them(Figure16). Rule 4 is applied to a data model with elimination. Figure 15 shows that if a user selects District and assigns a condition state_name = suwon, its associated class Parcel is selected by rule4. A user sets a reference field CODE between Parcel and District. Then rule 4 deletes references of parcel features that are associated with district features that are selected by elimination. Figure 17 shows that rule 4 replaces the value of CODE of a Parcel feature, which is associated with a district feature, with null.
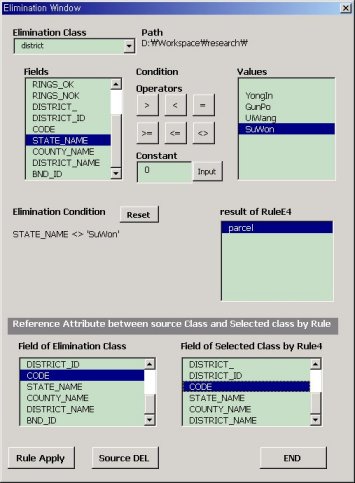
Figure15. select features for deleting.
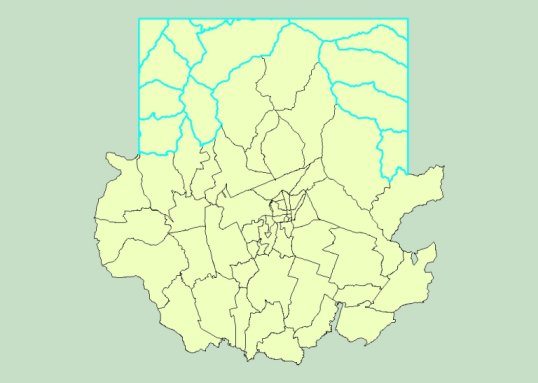
Figure 16. Features satisfy with a condition District. district_name = suwon
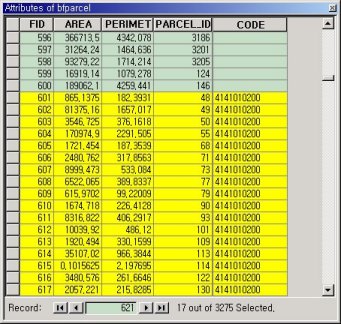
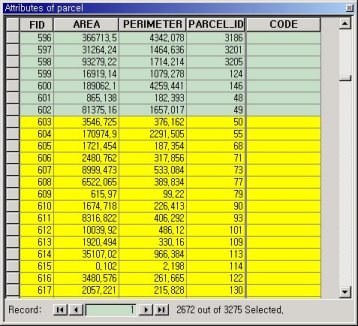
Figure17. Delete reference values by rule 4.
This operator is applied with rule 3, 7, 8 and 9 to a data model. In Figure 18, a user selects District, which is applied to classification, and State_Name, which is an classification item. Also a user assigns a new feature name State. Classification creates a new feature class State from District(Figure 20). This operator merges adjacent district features with the same value, into a new state feature.
Classification is applied with Rule3,7,8 and 9. Rule 7 creates topological relationships for State. A polygon topology is created. Rule 8 derives a new attribute from one of District. In this example, we do not specify an attribute to create new one. Rule 3 derives a domain for State. In this example, there is also no proper class. Rule 9 creates an aggregation relationship between County and District(Figure 19, 21).
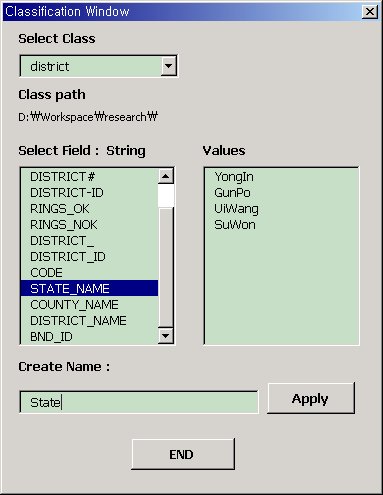
Figure 18. Classification interface
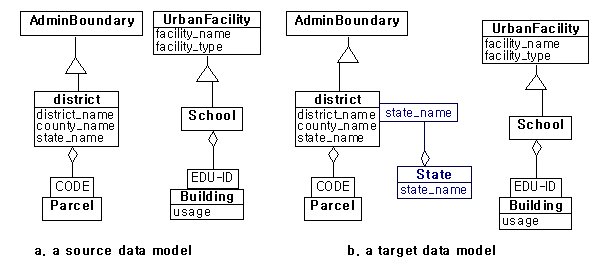
Figure19. Example(classification and rules)
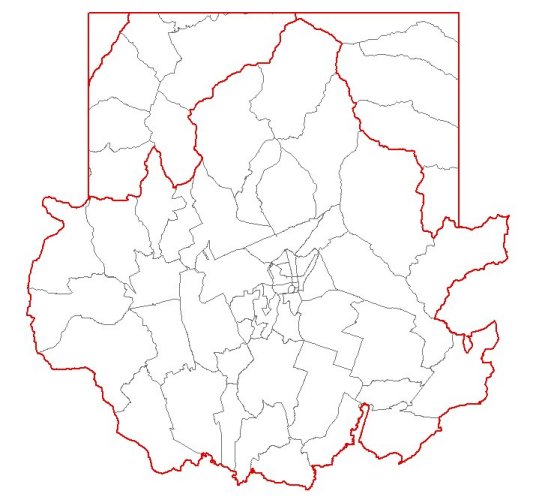
Figure 20. create new feature class State
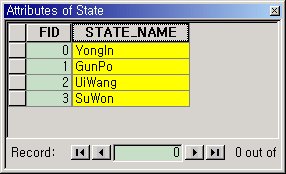
Figure 21. Create new attribute CITY
Simplification reduces details from district features. The tolerance is given as 100 for condition 3(Figure22). This operator is applied with rule 5 to a data model. Though the geometry of a district feature is changed, the topological relationships and topological consistency are preserved by rule 5. In order to preserve topological relationships, we simplify the geometry of an edge instead of the geometry of a polygon. In Figure 23 shows that point-edge and edge-polygon topology is preserved from simplification.
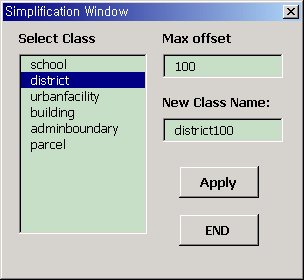
Figure 22. Preselection Interface
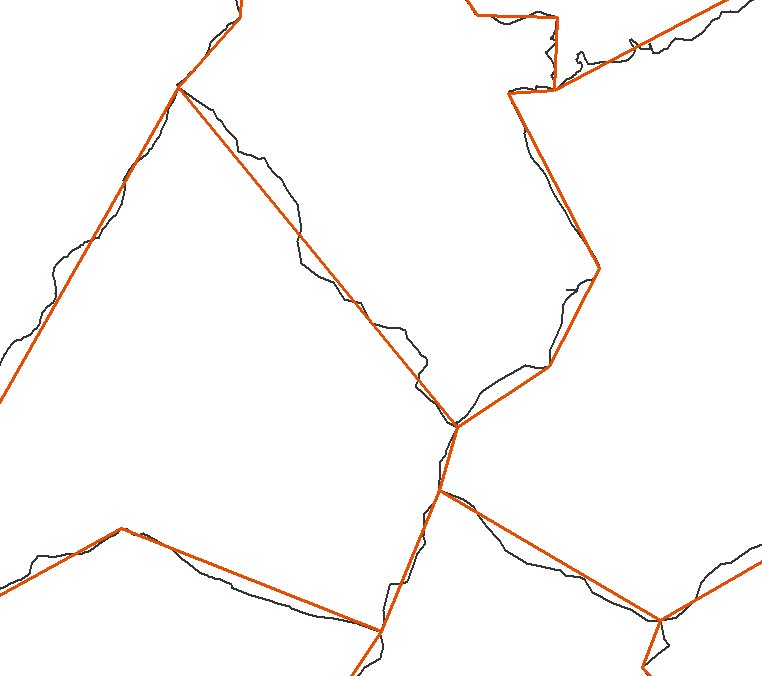
Figure 23. Preservation of topological relationship.
Though a number of researches have presented several methods of database derivation in GIS, they have been concentrated on the creation of a new feature class. To overcome this weakness, we first classified generalization operators into three categories(table3). Second, We proposed a set of rules which was useful to deal with the changes that occurred in the process of generalization. we developed a system to integrate these rules and generalization operators and increase the efficency of generalization activities on ArcInfo desktop 8.0.2 using ArcObjects and Visual Basic Application.
[Clodoveu94] Clodoveu A. Davis.Jr., K.A.de V. Borges, Object-Oriented GIS In Practice, 1994, URISA, Pages 786-795.
[Yee99] Yee Leung, Kwong Sak Leung and Jian Jhong He, A generic concept-based object-oriented geographical information system, I.J.Geographical Information Science, 1999, VOL.13, NO.5, Pages 475-498.
[Esri99] Michael Zeiler, Modeling Our World: The Guide to Geodatabase Design, Esri, Inc., 1999.
[Egenhofer92] M.Egenhofer and A.Frank, Object-Oriented Modeling for GIS,Journal of the Urban and Regional Information Systems Association 4(2):3-19, 1992.
[Worboys97] Micael F.Worboys, GIS A computing Perspective:4. Models of spatial information, Taylor & Francis, 1997, page 166.
[Rumbaugh91] James Rumbaugh et al, Object-Oriented Modeling And Design: 3. Object Modeling, 4. Advanced Object Modeling, Prentice-Hall, Inc., 1991, pages 21-80.
[Lag94] J.P.Lagrange, A.Ruas, Geographic Information Modelling: GIS and Generalisation, SDH, 1994, pp1100-1103.
[John99] John.G.Stell, and Michael.F.Worboys, Generalizing Graphs Using Amalgamation and Selection, SSD, 1999.
[McMaster92] R.B.McMaster, K.S.Shea, Generalization in Digital Cartography, The association of american geographers, 1992, p3.
[Esri96] Esri, Automation of Map Generalization, 1996, Esri.
[Tang96] A.Y.Tang, T.M.Adams and E.L. Usery, A spatial data model design for feature- based geographical information sustems, INT.J.Geographical Information Systems, 1996, Vol.10, No.5, pages 643-659.
[Beard91] K.Beard, W.Mackaness, Generalization Operations and Supporting Structure, Auto-Carto, 1991, Vol 10, pp35-39.
[John96] John.W.N, V.Smaalen, A hierarchic rule model for geographic information abstraction, 1996, SDH.
[Peng96] W.Peng, K.Tempfli, An Object-Oriented Design for Automated Database Generalization, SDH, 1996.
[Dettori96] G. Dettori and Enrico Puppo, How Generalization interacts with the topological and metric structure of maps, SDH, 1996.
[McMaster92a] R.B.McMaster, K.S.Shea, Generalization in Digital Cartography, The association of american geographers, 1992, pp72-98.
[Rigaux94] P.Rigaux, Michel Scholl, Multiple Representation Modelling and Querying, IGIS, 1994.
[Rigaux95] P.Rigaux, Michel Scholl, Multi-Scale Partitions: Application to Spatial and Statistical Databases, SSD, 1995.
[Barnett96] L.Barnett, J.V.Carlis, A Roads Data Model: A Necessary Component for Feature-Based Map Generalization, ACMGIS, 1996.
[Sester98]M.Sester, K.H.Anders, V.walter, 1998, Linkking Objects of different spatial data sets by Integration and aggregation, GeoInformatica.
[Ruas98] Anne Ruas, A Method for building displacement in automated map generalization, IJGIS, 1998.
[Richard94] D.E.Richardson, Generalization of Spatial and Thematic data using inheritance and classfication and aggregation hierarchies, SDH, 1994.
[Ooster95]P.V.Oosterom, V.Schenkelaars, The development of an interactive multi-scale GIS, I.J.GIS.
[Atzeni95] P.Atzeni, R.Torlone, Schema Translation between Heterogeneous Data Models in a lattice Framework, RT-DIA-27-1997, Technical reports at Department of CS and Automation, Roma TRE, , 1997.
[Atzeni97] P.Atzeni, R.Torlone, Management of Multiple Models in an Extensible Database Design Tool, RT-DIA-27-1997, Technical reports at Department of CS and Automation, Roma TRE, 1997.
[Nyerges89] T.L.Nyeerges, Schema integration analysis for the development of GIS database, IJGIS, 1989, pp153-183.
[Stefano99] C.Parent, S.Spaccapietra, Issues and Approaches of Database integration, CACM, 1999.
[Dettori98] G.Dettori, E.Puppo,Designing a library to support model-oriented generalization, ACM GIS, 1998.