The Best of Both Worlds:
Vector Conflation of Database Segments and Attributes
for Land Base Migration
Abstract
Conflation technology offers a cost-effective, efficient method of combining the best attributes of separate vector databases. Using GDT's proprietary conflation technology as a case study, this presentation will discuss how conflation techniques can assist in migrating a utility's facilities data from an existing land base onto a new land base. The presentation will provide an in-depth discussion of the challenges of matching elements within two distinct data bases, the hurdles that must be overcome, and the benefits of using conflation technology. The presentation will also highlight quality control issues such as preliminary database analysis and postconflation QC processes.
Introduction
Many utilities use a database of roads, boundaries, and rivers, often called the "base map" or "landbase", to which their facilities are spatially related. Facilities management (FM) applications place heavy demands on the land base system. We are seeing a growing need for land base systems to:
But the costs of maintaining that landbase or migrating to an improved landbase produce a strategic dilemma. The migration costs arise from the fact that facilities information is spatially related to landbase features, a relationship that often isn’t recorded with the data in a machine maintainable way. Thus, landbase migration is typically an extremely costly and error-prone process involving manually readjusting or realigning facilities. The dilemma comes down to two unsatisfying choices:
The first choice provides an arbitrary level of accuracy, but it’s expensive to maintain, tends to fail at interoperability, and may not contain the data attributes that can help provide an enterprise-wide solution. The second choice contains the maintenance cost, but it has historically been at the expense of accuracy and responsiveness to change – facilities get tied to inaccurate or old data, resulting in time and effort spent maintaining an inconsistent model. As commercial landbase quality and availability improves, the migration cost remains the chief barrier to incorporating the updates and improvements.
We will show a new way to help solve the problem, using conflation technology to automatically move facilities data that had been tied to one landbase, to align properly with another. The technique also generates QC points indicating where the process should be reviewed. As a result of this technology, the process costs can be dramatically reduced and the quality increased. The process can even be used to the upgrade the landbase on a regular basis, thus allowing you to keep up with the most current and accurate reference data available.
The remainder of this paper will be broken into three sections, to describe the three cooperating technologies that have been combined into a conflation solution that several large utilities have used successfully. Those steps are:
Conflation - Correlation
The first job of landbase migration is to understand how each feature in one landbase is represented in the other. Some features may not exist in both; some may be radically different, but once we build whatever legitimate relationships we can find, we’ll have a basis for comparison. This matching task is the crucial exercise in conflation.
Correlating features in two landbases requires these three steps:
Our approach has been to modularize the software and the process for each step listed above, allowing for individualized development, tuning, independent operation, and QC.
Prepare the Databases
The first matching task is to bring both databases into a common format, ensure that they are both topologically clean, and understand which if any data attributes will be available for the match software to use. Topologic cleanness – having a node at every line crossing – is important because intersection nodes are crucial elements of the match process. Data attributes such as name and feature type are useful because they add corroborating information that can heighten the confidence during matching.
We use automated and manual analyses to ensure the validity of matching, and ultimately the quality of the conversion. Our manual analysis uncovers which attributes are useful and reliable, and we convert or standardize them to improve the landbases’ compatibility with each other. Automated analysis takes the form of preliminary conflation match passes; we match the databases, and analyze the matched topology to find problems. This automated process often uncovers subtle topological errors in a landbase that can be corrected in the data. We may also uncover systematic differences in feature interpretation between the two landbase sources – information we can use in the next phase to guide the final conflation.
Build a Topological Representation
We build a topological representation from the selected features that we want to match in each landbase. The purpose is to:
Our topological representation ignores features that we have no interest in for conflation, or that are in some way incompatible. For example, customer data, parcel boundaries, rights-of-way, and certain non-road features will not have an equivalent in the Dynamap™ representation, so if they are present in the source landbase, they are of no use in matching to Dynamap™.
The topological model aggregates the remaining linear features to make meaningful "chains". For example, a chain of arcs representing a street centerline, running uninterrupted from one intersection to the next, could be aggregated based on operator-defined rules. An appropriate choice of aggregation rules is important for good conflation. For example, if both landbases record street name with a high degree of accuracy, then a name change along a street is an important event, and it should be considered a node between two distinct chains.
We also build additional information at this time. In particular, the software locates and marks multiple-carriageway roads. It assigns a directionality flag to indicate on which side the counterpart is found. This prevents ambiguity later, eliminating the possibility that the wrong lanes will be matched.
Matching
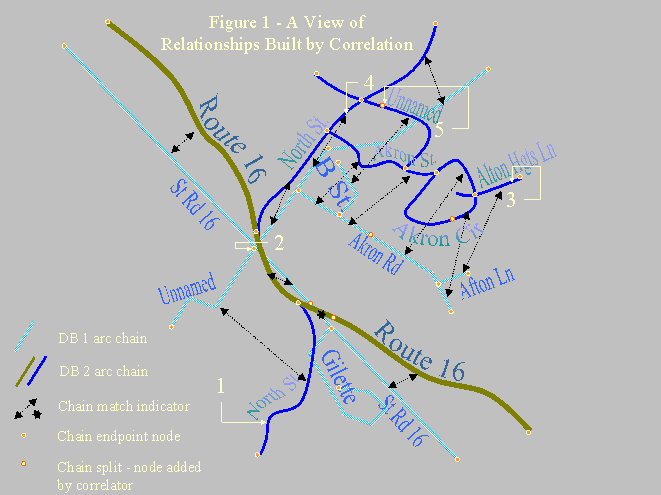
Figure 1 illustrates the basic challenge of matching. We see a view of two overlaid street centerline databases. At first glance, it seems that they represent the same area. We see a major road in each database, with a common route number and similar heading. There is a development to the northeast of that road in each case, with some similarity in names and geography. Even the crook in North St below the highway (label 1) bears enough similarity to that of the unnamed road to prompt a mental match, despite the difference in detail. But there are significant issues for software: roads are more angular in one database, lengths and proportions vary significantly, and streets that should match are not often nearest neighbors (label 1, North street, is a case in point). The following labeled areas illustrate other common challenges:How, then, do we build a reliable correlator?
We have had great success using a tunable multivariate stochastic model. To allow for wide variations in the quality of landbases we must match, the model includes well over 100 individually tunable parameters and sets of parameters. Some parameters can control the strength or presence of certain match objects or "agents," each of which specializes in analyzing a particular attribute or trait. Other parameters modify the mathematical formulae used by those objects to determine match likelihood. Still other parameters determine the level of confidence needed to declare a match in various situations. The model gives a weighted "vote" to each applicable agent to arrive at a final match probability, which ultimately determines the match decision.
We begin with node matching. Nodes are the confluence of a great deal of information, and are thus the places where pivotal matches can be assured. As with most other conflation software developers, we use iterative matching, choosing the strongest node matches in an early pass, and then conceptually rubber sheeting and using neighborhood information to match in repeated passes, continuing as long as new matches can be found. Node matching uses two match agents. One agent analyzes the candidate nodes’ rubber-sheeted offset and area density of nodes. A second attempts to build an optimal "test match" of all the feature chains that are incident at the node pair, to determine the similarity of the local features at the nodes.
Following node match, we use the matched nodes as a guide to matching our topologic chains. This stage is stochastic in nature, meaning that chains running between matched nodes aren’t necessarily rubberstamped as matches, and those running from matched nodes to unmatched areas may be split or even matched whole if doing so meets the operator’s match strength criteria. Finally, there may be chains with no topological (node connection) similarity, yet have strong match characteristics; we find and match these last.
Our chain match criteria include agents that weigh:
In addition, the following attribute-based match agents may be enabled if the associated attributes are available and reliable:
Generate Control Vectors and QC Points
With match information, we can generate a rubber sheet mapping for use in realigning associated facility data. We can also identify points where the mathematical model breaks because the topology has changed significantly or wherever there is a large amount of "shear" in the warp model.
Why QC Points?
To understand why QC points are needed – why the process cannot be 100% automatic – consider the extreme case of the transition shown in Figure 2, from an old landbase represented by the black street centerlines to the landbase indicated by the red centerlines. If the small development shown in each color is actually the same development, and the nearby intersection is also the same intersection, then the two landbases have a major contention as to the order of the intersections. This could occur in the real world due to development of the major roads, or it could be a result of a landbase error. When a facility lies between the intersections in the old database shown below, where should it be relocated? The answer depends upon what that position really meant: did it mean "to the east of the major intersection", or "between the two intersections", or "to the west of the entrance to the development"?
Such ordering differences and other topological differences cause areas of ambiguity, inversion, or collapse in any mathematical model. When an inaccurate landbase had been used, the reality is that some manual interpretation or adjustment must have occurred in the earlier, less accurate database, to relate real world objects with inaccurate landbase components. That interpretive step loses information about real world relationships that warping algorithms alone aren’t able to restore.
We expect these cases to be rare, but locating them is important! This is why QC points that highlight extreme distortion, sheer, or topology difference are crucial to an effective migration. We want to confidently migrate most of the data to a new landbase, and focus only on the areas where a problem may have occurred.
Control Vectors and Constraint Lines
The raw mathematical model we generate to move facilities to a new landbase is based on
These concepts are illustrated in Figure 3. (A) All conflation-matched arcs from the old landbase form the basis for the control vectors and constraints. (B) Using a linear interpolation, each shape point on an arc or its match is associated with the equivalent point along the correlated arc. These point relationships are the control vectors. In actual practice, the control vectors are often generalized slightly to reduce the machine effort in realignment, and to reduce the control vector file size. (C) This combination of control vectors and constraints is sufficient to record the movement of all known features; it forms the basis of a planar map defining movement for any related objects.
Figure 3 also illustrates the value of constraints. Movement that is indicated on one side of a chain of matched objects should not affect objects that are on the other side of the chain. Constraints prevent house #1 in figure 3 from being "pulled" to the wrong side of the road by the strong easterly displacement of an unrelated nearby street, despite the fact that that control vector is physically the closest to the house.
A final component of the data is fixed vectors, or "zero move" vectors. These vectors map some point in the plane to itself, so they define limits of realignment. We generate these by building a fixed-distance buffer around all moved objects. We typically set this buffer width to 1200 feet. This means that any object in the facilities or related data set is not affected by landbase arc changes that are more than 1200 feet away.
Realign Features
Automated realignment can now take all related point, line, and polygonal objects and translate them to the most logical place in the new landbase. When you migrate from a relative spatial model to a spatially accurate model, there is no algorithmic way to use the crude data to accurately place facilities at real world coordinates. However, automated realignment is a very valuable first step to move facilities into a relative conformance with the new landbase. A readily available solution is Safe Software’s FME™ translator, which has a module that relocates facilities based on our control vectors and constraints. GIS personnel could also build custom tools, such as AML scripts using ARC’s "adjust" command or other techniques mentioned below, to perform the realignment.
There is much academic literature on models for planar interpolation. Kriging and triangulation approaches work well, as does "gravity based" inverse distance model, which is employed in Safe Software’s FME™ translator. The gravity-based model has the advantage of tunable parameters to calculate the relative effect of nearby control vector points on any point. Constrained Delaunay triangulation is an excellent technique that can uniformly interpolate the plane, regardless of the control vector density, but it is a linear transformation that isn’t tunable.
Future enhancements of our control vectors package may include placing specific information on each control vector regarding which landbase feature(s) it represents. This could further improve the migration of any facilities data where there is a defined relationship with a landbase component.
Any automated model will fail to resolve all ambiguities, since our knowledge of the plane is incomplete and based only on the matched landbase objects. The QC points highlight such questionable areas; any movement that has been affected by a control vector coincident with such a QC point should be manually inspected.
Conclusions
The cost of Landbase migration can be greatly reduced through the use of conflation technology and a maturing body of interpolation algorithms.
Drawing on the techniques outlined here, GDT has successfully helped a number of major utility companies to move from older, privately maintained landbase data to more accurate and less costly-to-maintain commercial landbase data. In addition, our own product is now delivered with release-to-release control vectors, allowing incremental update wherever we realign and improve our data. Though interpolation techniques aren’t flawless, they can easily reduce migration costs by 80% or more, and with use of QC points the problem areas are easy to spot.
Automated landbase migration technology has proven to be a cost-effective tool to enable utility GIS departments and conversion vendors to keep landbase and facilities data in harmony.
Author Information
Alan Witmer
Senior Software Engineer
Geographic Data Technology
11 Lafayette St, Lebanon, NH, USA 03766
Telephone: (603) 643-0330
E-mail: alan_witmer@gdt1.com