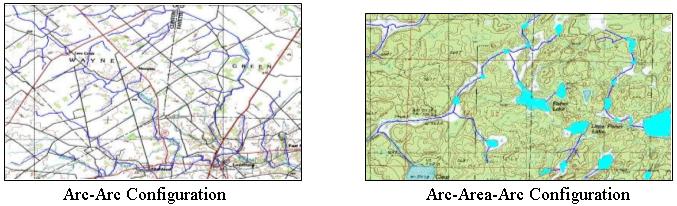
Figure 1. Hydrological networks configuration.
Traditionally the modification of scale is a manual process. The Geographical
Information Systems (GIS) provide tools in order to make it, however like
in manual process this depends on the experience of the users and how these
tools are used. Implementing a method that can work automatically allows
us to obtain consistent results, according to established rules. The cartographic
generalization establishes rules to preserve the geometric and semantic
characteristics of the objects. In this work we consider the scale modification
from 1:50,000 to 1:250, 000. The process of change of the scale requires
the following stages: Analysis, Automatic Correction of Arc Directions,
Classification, Selection/Elimination, Simplification and Enhancement.
The Automatic Correction of Arc Directions is a very useful function that
requires only an altitude layer. The classification is denominated CLAJER.
It orders the arcs of the network by their length. This process has been
evaluated for real maps in order to find some inconsistencies in the change
of scale. This system has been implemented in Arc/Info by means of AML
codes.
In the context of digital cartography the generalization has obtained
even wider meaning. It means the possibility to flexibly select and compose
feature classes. The features are obtained from queries, the interactive
zoom and the inspection of the data at any desired scale (magnification
and reduction). The use of GIS for implementation of a system able
to generalize allows us to obtain consistent results, according to established
rules. In the context of GIS, the generalization implies the application
of attribute (database) and spatial (geometric) transformations. Database
modification includes: the number of entities reduction; attributes elimination;
attribute values robustness. Spatial transformations imply the reduction
of object density (or its parts) and simplification of the shape. All these
aspects are considered in this work.

Figure 1. Hydrological networks configuration.
Due to problem's complexity, the analysis is focused to modify the scale
in the networks with the arc-arc configuration. In the following works
it would be possible to consider any configuration of networks, using the
flow direction. To modify different configurations it is required to manipulate
any vectorial layers since the lakes and rivers are stored in different
layers. When the scale changes, the representation of some objects (principally
lakes and rivers) may be is changed too. The map projection of vectorial
layers used in this work has to be UTM or any other projection in meters
units.
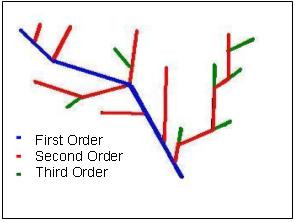
Figure 2. Hierarchical Length Classification (CLAJER).
The classification is an evaluation of the possible routes that can
follow the flow from all the inputs to the output. It can iteratively
be applied, since the same principle is used to find all orders. This classification
allows preserving the characteristics of the Hydrological Network.

Figure 3. Selection criteria.
The Douglas-Peuker algorithm is used to simplify the arcs. This step eliminates some vertex to be considered unnecessary after modifying the scale. This algorithm allows us to obtain a good map simplification. In addition it preserves directional trends in a line using a tolerance factor which may be varied according to the required simplification degree. To obtain a better visual quality the arcs are smoothed using Splines in order to produce more aesthetically shape and eliminate some effects of simplification. Both functions represent the generalization operators and cause displacement in coordinates pairs. The displacement solely acts on each one of the arcs, but not on the path (composed of many arcs). This is why the coordinates of the nodes are preserved. The nodes must be eliminated to simplify the database to the maximum. Each pair of nodes represents a register. The nodes are not eliminated before Simplification and Enhancement operators are executed.
This method is implemented in ARC/INFO, using AML. ARC/INFO provides the functions that can be used to implement generalization systems as BUFFER, CLIP, Line simplification, etc. It has good capacity to make operations on the database. It can be implemented in wide classes of GIS. Figure 4 shows the general process of the generalization step by step.
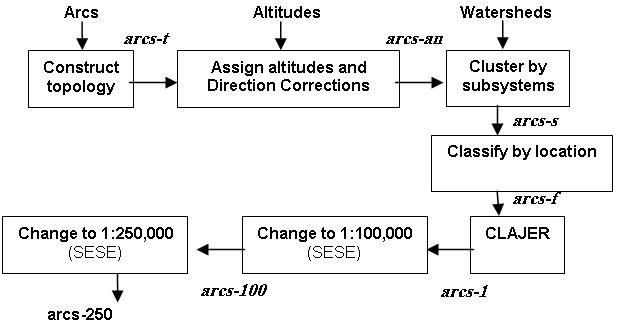
Figure 4. General process of the generalization.
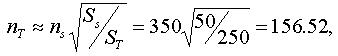
Figure 5. Equation of the radical law.
Where:
nS - Number of objects in source map;
SS - Source scale;
ST - Scale after transformation;
nT - Number of objects in map after transformation.
These results have visually been analyzed and compared with manual INEGI
data, it is observed that in the resulting map the main flows preserve:
Figure 6(b). Based on test results, we can apply these criteria to change
different scales just modifying the criteria of selection and the tolerances
of simplification and enhancement. The significant differences are originated
due to the extension and number of objects in the network. Better results
would be obtained if more extensive areas and objects are considered.
In the Figure 7 is shown the Graphical User Interface (GUI) of the system. This GUI contains the main functions in order to generalize spatial data in an automatic way.
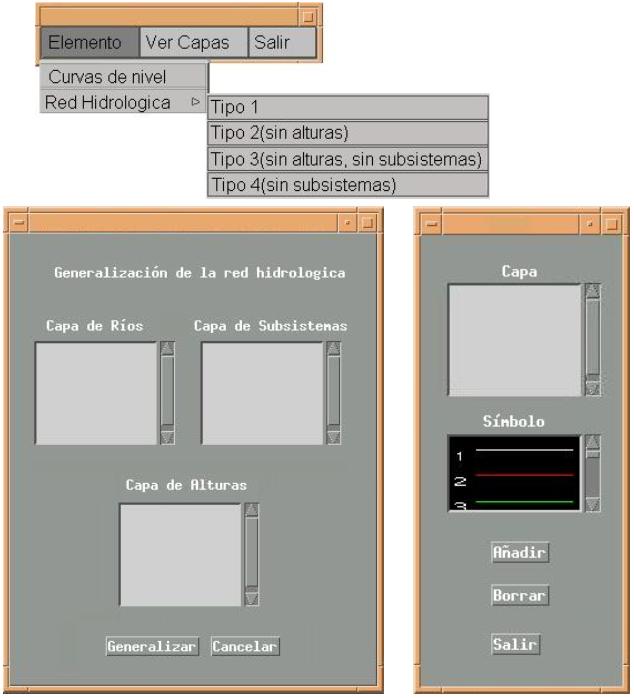
Figure 7. The GUI of the system.
The process can be executed without additional information to spatial data. It is only required the correction of connections between arcs and the directions of the flow. The arcs can automatically be corrected, using only altitude layers. Furthermore in the classification processes the additional information has been generated. CLAJER allows us to modify the objects topology and graphics. The semantic value of the network is preserved.
At this moment, it is possible to change the scale in automatic way
for the arc-arc configuration. In the following, it would be possible to
process other configurations, using the flow representation in order to
quantify the network. In addition it is necessary to develop a process
to collapse automatically areas and automatically represent the flow, using
the information from several layers. It is necessary to consider, the information
from other topics such as populations and roads.
[1] Environmental Systems Research Institute Inc., "ARC/INFO User
Guide: Map Display and Theory", Redlands, California, Esri, Inc. 1993.
[2] Environmental Systems Research Institute Inc., "ARC/INFO User Guide: ARC/INFO Data Model, Concepts and Key Terms", Redlands, California, Esri, Inc., 1997.
[3] Frank U. Andrew, Werner Kuhn, "Spatial Information Theory (A Theoretical Basis for GIS)", International Conference Cosit Helsinki, 1995.
[4] National Institute of Statistics, Geography and Informatics (INEGI), "Diccionario de Datos Topográficos (Vectorial) Escala 1:250,000", México, 1998.
[5] National Institute of Statistics, Geography and Informatics (INEGI), "Diccionario de Datos Topográficos (vectorial) escala 1:50,000", México, 1998.
[6] Kilpeläinen Tiina, "Map Generalisation in the Nordic Countries", Geodetiska Institutet, Helsinki, 1999.
[7] Kilpeläinen Tiina, "Multiple Representation and Generalization of Geo-Databases for Topographics Maps", Geodetiska Institutet, Helsinki, 1997.
[8] Kilpeläinen Tiina, "Multiple Representations and Knoledge-based Generalization of Topographical Data", Geodetiska Institutet, Helsinki, 1992.
[9] Molenaar Martin, "An Introduction to the Theory of Spatial Objects Modeling for GIS". Taylor & Francis, 1998.
[10] Moreno M., "La Generalización Automática de la Información Geográfica Multiescala", Centre for Computing Research, National Polytechnic Institute, Mexico, D.F., 2001, (M.S. Thesis in Spanish).
[11] Müller Jean-Claude, "GIS and Generalization", Taylor & Francis, 1995.