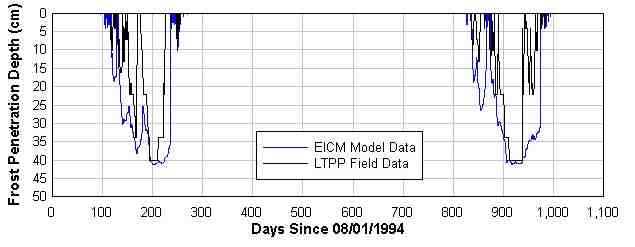
FIGURE 1. Plot Showing Comparison of Numerically Modeled Frost Penetration Depth with Freezing Depth Inferred From LTPP Field Data at Section 50-002, New Haven Junction, Vermont.
Stephen P. Farrington, P.E.
Applied Research Associates, Inc.
415 Waterman Road, South Royalton, Vermont 05068
phone: 802-763-8348
fax: 802-763-8283
email: sfarrington@ned.ara.com
Martin L. Gildea
Applied Research Associates, Inc.
415 Waterman Road
South Royalton, Vermont 05068
phone: 802-763-8348
fax: 802-763-8283
email: mgildea@ned.ara.com
A novel methodology was developed using numerical simulation, statistical regression, spatial interpolation, and GIS to predict maximum frost penetration depth in a typical pavement structure throughout the state of Vermont at different levels of statistical reliability. The methodology behind historic maps of frost penetration was unknown and did not appear to incorporate the influence of elevation, a key determinant in air temperatures affecting pavement surface cooling. New maps, developed in ArcView, will be used to design pavements for new road construction, which must extend to a specified percentage of the maximum frost penetration depth.
The formation of frost in pavements has the potential to cause pavement damage. Many pavement design criteria specify the minimum depth of the pavement structure as a function of the maximum frost penetration depth. In designing new pavements, the Vermont Agency of Transportation (VAOT) had in the past relied on maps of statewide frost penetration developed some 30 or more years ago. The methodology and sources of data for the maps were not known, and their reliability was uncertain. A methodology was developed using a combination of numerical modeling, geostatistics, and linear regression to produce new maps at 50% and 90% statistical reliability.
The formation of frost in pavement structures is of engineering concern because of the potential to cause damage due to differential volume changes. These changes are caused during freezing by increases in moisture content, the conversion of water to ice, and formation of ice lenses. Appropriate pavement design can avert frost damage by (a) reducing moisture through improved drainage (and diminished capillarity), (b) controlling pavement thermal properties, or (c) a combination of moisture and thermal control. Many pavement design procedures specify the depth of the structure to be a percentage of the maximum frost penetration depth. The depth to which frost will penetrate a pavement structure, however, is controlled to a large degree by the design of the structure. Additionally, frost penetration depth in a pavement structure will be greater than in a snow-covered profile, due to the thermal insulating properties of the snow.
Frost forms in soils when the temperature of the soil matrix falls below the freezing point of bulk water, causing water present in the pore spaces to freeze. The freezing process occurs gradually and is the result of the loss of heat through the soil or pavement surface to the cooler air above. Anywhere there is moisture in the soil at temperatures below the freezing point of the contained water, frost occurs. Kane and Chaco (1) present an overview of the physical basis for frost formation in soils, while Holtz and Kovacs (2) give an account of historic developments in the understanding of soil freezing phenomena and their impact on engineered structures.
Frozen soil may consists of soil, air, unfrozen water, and ice. Even at temperatures well below the freezing point of bulk water, some unfrozen water may remain in the soil. The amount of unfrozen water depends not only on the temperature depression, but also on the specific surface area and salt content of the soil. The smaller the soil particles, the greater the proportion of unfrozen water at a given temperature below freezing. The presence of unfrozen water is significant because it provides the opportunity for moisture to migrate vertically, enabling the formation and thickening of ice lenses. Ice lenses are horizontal layers of solid ice that form below the ground surface, separating the soil above from that below. They pose the greatest potential for damage due to the magnitude of displacements they cause in the pavement structure and are the phenomenon responsible for frost heaves.
Heat and moisture migrate in soil in response to temperature and suction gradients, respectively, with the flow of both occurring from warm soil to cold soil. As a soil freezes due to loss of heat to the atmosphere, the heat and the moisture migrate toward the surface. The upward migration of water is due to the decrease in the partial pressure of water with respect to the pore fluid matrix that occurs at the freezing front as liquid water is converted to ice. This loss of water due to freezing is analogous to drying, which induces a suction gradient. The migration of moisture is further enhanced by the order in which pore water freezes. The unfrozen water remains in a thin layer around the individual soil particles, while the already frozen water occupies the regions of the pore space farthest from the soil grain surfaces. Thus, capillary potential is enhanced by the effective decrease in porosity that occurs as freezing progresses in the pore space, as well as the increased surface tension of water at reduced temperatures.
Eventually, sufficient ice may form in the pore space to create a barrier to moisture migration. This is when ice lenses form, because migrating water becomes trapped at the freezing front, which forms the terminus of its upward migration to "drier" soil. The formation of ice lenses tends to be initiated where porosity is already low, such as in layers of silt or clay. Ice lenses can grow to several centimeters in thickness, which translates directly into displacement of the pavement.
The simplest approaches to predicting frost penetration utilize freezing degree day indices. There is a physical basis to this approach because the air temperature significantly influences the thermal boundary condition at the surface of the pavement, and thus the gradient to which heat and moisture flow respond. However, air temperature at the surface is not the only variable controlling pavement cooling. Other variables include: (a) the thermal conductivity of the pavement surfacing materials; (b) the thermal conductivity of the pavement sub-base, which is greatly influenced by moisture; (c) air thermal capacity, as controlled by temperature and humidity; (d) wind speed; and (e) solar radiation, which can generate heat in a pavement surface even as the air is cooling it.
Increasing the complexity of the frost prediction problem is the influence of moisture. Freezing of a pavement structure is the result of the dual migration of heat and moisture. Therefore, the rate at which the soil freezes will influence the depth and impact of frost penetration more profoundly than the final temperature profile of the soil. For example, during a rapid freeze moisture may not migrate quickly enough to feed the formation of an ice lens, whereas during a slower freeze it may. Even though temperatures will likely be more extreme during the rapid freeze event, frost damage due to moisture wicking might actually be greater during the slow freeze. Conversely, an intermittent thaw at the ground surface may cause released water to drain to a colder depth where it re-freezes, causing the initiation of an ice lens by restricting the pore space. Furthermore, the role of soil moisture is amplified by its dramatic influence on the thermal conductivity of the subgrade.
Factors dynamically affecting the soil moisture content in a pavement structure include: (a) the initial moisture condition; (b) boundary moisture conditions; (c) precipitation and infiltration; (d) pavement cross-sectional geometry and drainage characteristics; and (e) material gradations.
Due to the role of dynamically changing soil moisture in frost penetration, freezing degree day indices alone rarely provide reliable prediction of frost penetration in pavement structures. A site-specific correlation to freezing degree index, based on local climatic and moisture conditions, may prove more useful. The most sophisticated methods for predicting frost penetration incorporate knowledge of soil moisture content with varying degrees of complexity. Some also include damage models that predict frost heave and thaw settlement. Varying degrees of sophistication can be employed to predict frost penetration. The appropriate degree of sophistication for any frost penetration prediction depends on the intended use of the resulting prediction, the availability and reliability of relevant input data, and the sensitivity of the resulting prediction relative to uncertainty in the input data.
The method used to predict statewide maximum frost penetration depth utilized numerically modeled mechanistic predictions of frost penetration from actual climatological records over a 40-year period (1950 to 1990) in a typical pavement at each of 6 meteorological observation stations scattered throughout the state. The resulting 240 predictions of annual frost activity were then regressed against actual annual freezing degree index (AFDI) at these 6 stations. The regression equation was then used to relate frost penetration depth, specific to the pavement modeled and the weather dynamics of the region, to AFDI at the 50% level of reliability. Similarly, this exercise was repeated for the 90% reliability level using the regression of the one-tailed 90% upper confidence limit of penetration depth on the one-tailed upper 90% confidence limit of AFDI from all stations modeled.
To ensure a stable meteorological record for predicting frost penetration at the two levels of statistical reliability desired, the stability of the Vermont climate over the past several decades was first evaluated. Meteorological data from six pre-selected weather observation stations scattered throughout the state were analyzed for temporal trends in annual freezing degree-days. A linear least squares regression was performed on these data relating annual freezing degree index (AFDI) to year of occurrence. The average R-squared of the six regressions relating AFDI at each station to year of occurence was 0.019, indicating that less than 2% of the variability in the AFDI over the period examined is correlated to the year of occurrence. One can therefore conclude that the local climate was stable enough that frost penetration predictions can be reliably based on the 40 years of available climatic data.
The Enhanced Integrated Climatic Model (EICM), version 2.6, was used to model frost penetration in a typical pavement under actual meteorological conditions over a period of forty years at the six meteorological stations utilized for the climatic trend analysis. The pavement specification was provided by VAOT.
EICM, developed jointly by the University of Illinois at Urbana-Champaign and the Texas Transportation Institute, Texas A&M University, is among the most sophisticated models available for predicting frost penetration in pavements. EICM is a two-dimensional coupled heat and moisture flow program for analyzing pavement soil systems in conjunction with climatic conditions. The model combines three separate models of climate effects on pavement: (a) the Climatic-Materials-Structures Model (CMS) developed at the University of Illinois; (b) the Infiltration and Drainage Model (ID) developed at Texas A&M University; and (c) the Frost Heave and Thaw Settlement Model developed at the United States Army Cold Regions Research and Engineering Laboratory (CRREL). EICM accepts actual meteorological data as input and has a variety of options for specifying moisture and temperature, or their flux, at the lower boundary and at the interface between the subbase and the subgrade. It considers the lateral and vertical drainage of the base, which is a two-dimensional problem, in determining the amount of water that enters the subbase by infiltration through the pavement surface and base. Version 2.6 of EICM also improves the model's soil moisture calculations by introducing the Fredlund-Xing relationship as a user-selectable alternative to the Gardner functions.
Field data from the Long Term Pavement Performance (LTPP) project obtained from a test section at New Haven, Vermont were used to verify results from EICM. This section had been instrumented with a weather station, and temperature and electrical conductivity arrays prior to 1994. The instrumentation layout is described by Ali and Tayabji (3). Data from the section were available on CD-ROM distributed by the Federal Highway Administration for the years 1994 through 1997.
The model was run assuming the pavement structure specified by VAOT for the mapping exercise, and utilizing as other inputs the New Haven Junction weather station data from the LTPP DataPave CD-ROM. At this location, the actual depth to groundwater of about six feet, available from DataPave, was utilized. FIGURE 1 illustrates the agreement between the model predictions and actual field data. The actual depth to freezing was interpreted from the LTPP data as the depth at which the soil temperature in the profile transitioned from less than -2.2°C to greater than -1.1°C. This transition point is below 0°C due to salinity, and was chosen based on interpretation of changes in the resistivity profiles following the onset of sub-zero weather. The maximum seasonal frost penetration depth predicted by EICM agreed to within 3 cm of the maximum depth inferred from the temperature and resistivity profiles.

FIGURE 1. Plot Showing Comparison of Numerically Modeled Frost Penetration Depth with Freezing Depth Inferred From LTPP Field Data at Section 50-002, New Haven Junction, Vermont.
EICM was also evaluated for sensitivity to variation in several climatic parameters. The sensitivity analysis was conducted by repeatedly modeling the behavior of the same pavement while varying several climatic parameters and pavement thermal properties one at a time. The analysis showed that the maximum seasonal frost penetration predicted by EICM was relatively insensitive to variations in depth to water table, percent sunshine, wind speed, and pavement surface absorbtivitty. Thus, potential inaccuracies in the assumed and/or estimated values for these parameters would not significantly impact the study outcome. The results of this analysis are discussed thoroughly in the final report of the project (4).
EICM requires the specification of climatic data, a pavement structural geometry, and pavement material properties, including porosity, dry density, thermal conductivity, saturated permeability, and gradation information, as well as solar absorption coefficient for the surface layer.
For climatic data, EICM requires maximum and minimum air temperatures, wind speed, percent sunshine, daily rainfall, station latitude, and depth to groundwater. Climatic data came from a National Climatic Data Center (NCDC) data product, "Cooperative Daily Summaries." Location-specific data for a few climatic parameters were not available from this product, so a constant wind speed of 10 mph and constant percent sunshine of 60% per day were assumed for all model calculations, except during model validation using the New Haven Junction test section, where these data were available from the LTPP project. The LTPP data also formed the basis for estimating the sunshine and wind speed inputs used for the rest of the stations. Depth to groundwater was assumed constant at 10 feet throughout the state. Although, according to the sensitivity analysis performed on EICM, a shallower water table would have resulted in slightly more conservative predictions (i.e., deeper frost penetration), the change due to even a halving of the water table depth is relatively inconsequential (1.6%).
The model pavement, as specified by VAOT, was composed of 20.3 cm (8 in) of asphalt concrete, with 61.0 cm (24 in) of A-1-a crushed stone base course, and 40.6 cm (16 in) of subbase of A-3 sand for which a gradation curve was available. Beneath the pavement, an A-4 silt was assumed to a depth of 610 cm (20 ft) (i.e., to the deep ground temperature boundary condition). Typical values of thermal, hydraulic, and other material properties were used for the pavement material inputs to EICM. These values are shown in TABLE 1.
TABLE 1. Pavement Properties Used as Input to EICM.
| Layer | ||||
| Surface | Base Course | Subbase | Subgrade | |
| AASHTO Material Designation | ACC | A-1-a | A-3 | A-4 |
| Thickness (cm) | 20.3 | 61.0 | 40.6 | 487.7 |
| Thermal Conductivity (joules/hr-cm-C) | 41.8 | 25.1 | 20.9 | 16.7 |
| Heat Capacity (joules/kg-C) | 919 | 877 | 836 | 836 |
| Unit Weight (kg/l) | 2.37 | 2.11 | 1.84 | 1.76 |
| Porosity | n/a | 0.25 | 0.30 | 0.40 |
| Saturated Permeability (cm/min) | n/a | 50.8 | n/a | 0.003 |
| D60, mm | n/a | 20 | n/a | n/a |
| Percent passing #200 sieve | n/a | n/a | 7 | 70 |
| Plasticity Index, % | n/a | n/a | 0.1 | 5.0 |
All model runs evaluated periods beginning August 1, to give adequate time for the influence of dynamic input data to fully obviate initial guesses of moisture and thermal profiles before the onset of frost-inducing surface meteorological conditions. Runs were ended on July 30. A program was written in C++ to extract the maximum seasonal daily frost penetration depth from each year of output (August through July) in the EICM thermal output (.thm) files.
The AFDIs corresponding to the 40 numerically modeled seasons of data at each station were also calculated from daily observations. As with the numerical modeling, the season for the AFDI calculation was defined at August 1 to July 30. These AFDI values were used to perform a linear regression of the modeled seasonal maximum frost penetration depth on AFDI. The least squares fit is shown in FIGURE 2, along with the upper 90% one-tailed prediction limit.
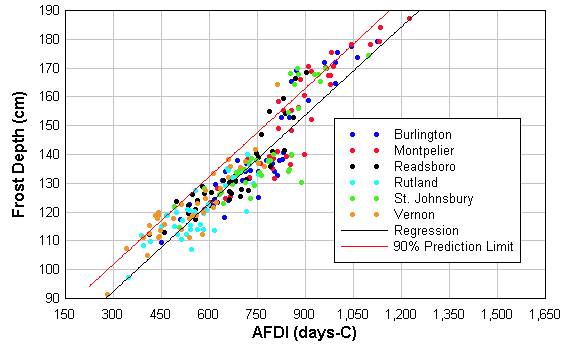
FIGURE 2. Plot of Correlation Between Modeled Frost Penetration Depth (D) and Annual Freezing Degree Index (AFDI) Calculated from Actual Meteorological Records at Six Stations, with linear regression and one-tailed upper 90% prediction limit.
The equation relating frost penetration to AFDI, in Celsius degree-days is:
D = 62.2 + 0.1024 AFDI (1)
where D is frost penetration depth in centimeters. The value of R-squared for this correlation indicates that 86% of the variability in frost penetration depth is predicted by variability in AFDI on a seasonal basis.
To develop the 50% reliable maximum frost penetration depth from the regression of D on AFDI, the regression equation was used, because the actual frost penetration depth in any given year has a 50% chance of being less than predicted by this equation. Therefore:
D50 = 62.2 + 0.1024 AFDI (2)
To develop the 90% reliable correlation between AFDI and frost depth, the upper 90% one-tailed prediction limit was used, since by definition the actual frost penetration depth in any given season would have a 90% probability of being below that predicted by this limit. This is the same as the upper limit of the 80% two-tailed prediction interval (e.g., 80% probability of being between the upper and lower bounds of the 80% prediction interval and 10% probability of being below the lower bound of the interval).
D90 = 71.4 + 0.1024 AFDI (3)
ArcView GIS was used to convert a 1000-m resolution statewide grid of mean AFDI to D50 and D90 using equations (2) and (3). These resulting D50 and D90 grid layers were then used in the production of maps of seasonal maximum frost penetration depth at the two reliability levels.
A 100-m resolution statewide grid of mean AFDI was produced using data from 17 meteorological observation stations throughout the state. These data were processed to calculate the mean AFDI and the one-tailed 50% and 90% upper confidence limits at each station. Of over 350 meteorological observation stations within the state, only these 17 met the criterion of possessing a minimum 49-year data record that was at least 73% complete (i.e., only stations having a 36-year span or more out of the possible 49-year span were included). A freezing index maps was produced by multivariate linear regression of AFDI against X, Y, and Z (e.g., easting, northing, and elevation) station coordinates with spatially interpolated residuals subtracted from the regression prediction.
The regression of AFDI on X, Y, and Z resulted in an R-squared value of 90%, with residualsmaking up about 10% of the variability in AFDI. The residuals are a result of conditions not included in the analysis and not available within the data currently available (i.e., factors other than X, Y, and Z). These factors may include orographic effects (hollows and "cold spots" due to topography), distance to large water bodies, and details of temperature stations. The specific linear relationship found was:
AFDI = -426.1 + 0.0017785 X + 0.0013451 Y + 0.6585278 Z (4)
where X, Y, and Z are Vermont state plane coordinates in meters (NAD83 projection) and AFDI has units of Celsius degree-days. The 17 station residuals were then spatially interpolated over a 1000-m statewide grid using inverse distance weighting. In inverse distance weighting, the influence of any known point on the interpolated value of an unknown point is proportional to the inverse of the distance between them. The interpolated residuals grid was then subtracted from the multivariate linear regression grid to produce an AFDI that was the sum of (a) the regression model and (b) an inverse distance-weighted interpolation of the residuals. In this way, the data at the 17 known stations are respected (exactly interpolated).
Equations (2) and (3) were used to transform the mean AFDI coverage to maximum frost penetration depth at 50% and 90% reliability. Although the 90% reliability level is more typically what is required for pavement design, the map at 50% reliability was produced for comparison to the original frost penetration maps (c. 1960). All maps are presented in U.S. customary units for comparison to the historic map, which was available only in these units. The map for the 50% reliability level is shown in FIGURE 3, with the corresponding pre-existing map appearing in FIGURE 4, and the calculated difference between the old and new appearing in FIGURE 5. As the figures illustrate, much greater spatial detail is available from the newer maps, which provide predictions of as much as 38 cm (15 in) deeper and 64 cm (25 in) shallower than the previous maps. The map of maximum frost penetration at the 90% reliability level is shown in FIGURE 6.
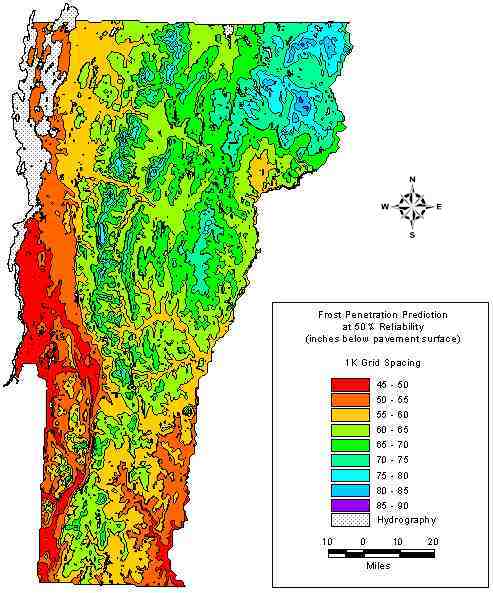
FIGURE 3. Predicted Statewide Maximum Frost Penetration Depth in Inches at 50% Reliability.
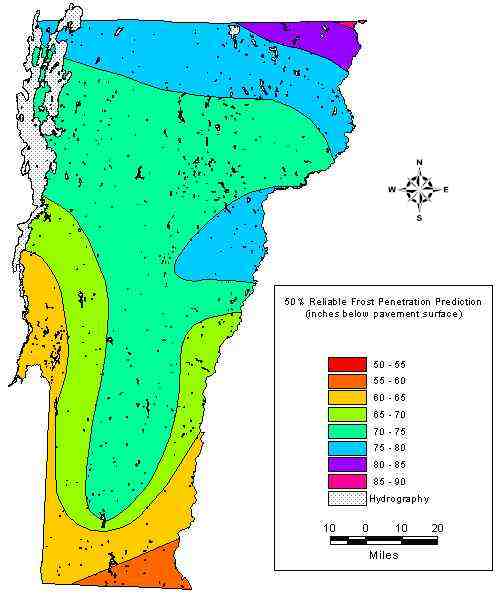
FIGURE 4. Pre-Existing Map of Statewide Maximum Frost Penetration Depth in Inches at 50% Reliability.
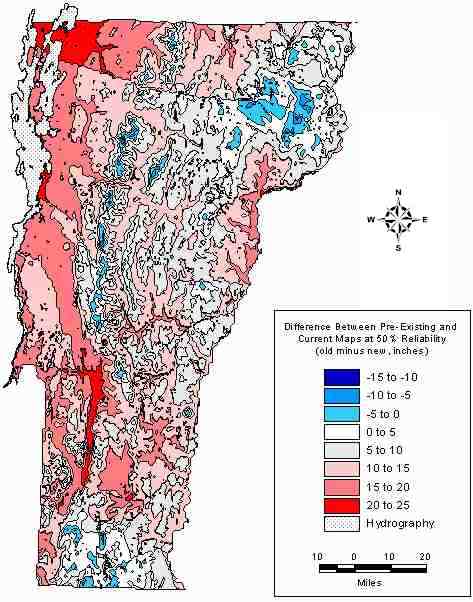
FIGURE 5. Difference Between New and Pre-Existing Map Of Statewide Maximum Frost Penetration Depth in Inches at 50% Reliability.
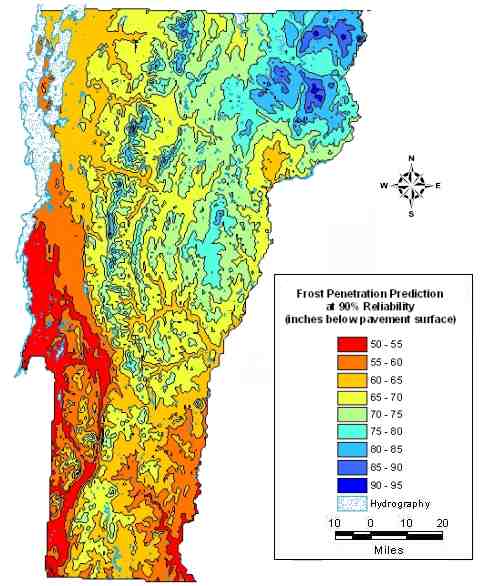
FIGURE 6. Predicted Statewide Maximum Frost Penetration Depth in Inches at 90% Reliability.
Based on the analyses conducted, one may conclude that seasonal maximum frost penetration depth can be reliably estimated by a relationship to AFDI, as long as a pavement-specific relationship is derived using meteorological data that account for region-specific weather dynamics. A regression of maximum seasonal frost penetration depth (derived from dynamic simulations of temperature and moisture flux in a pavement structure using actual climatic data) on AFDI showed a strong positive correlation and was useful for fitting a linear equation to the median and 90% upper prediction limit of maximum frost penetration depth.
No statistically significant change in climate has occurred throughout the state of Vermont over the past several decades. No trend was discernable at the 95% confidence level at six meteorological stations evaluated throughout the state, and less than 2% of the variability in AFDI is correlated to the year of occurrence. AFDI is therefore a stable metric for use in frost depth predictions. However, no field data were available to validate the equations relating seasonal maximum frost penetration depth to AFDI in the pavement modeled. This is recognized as a limitation of the work described.
Examination of the statewide maps of AFDI and annual maximum frost penetration depth that were produced indicates that significant spatial variability is present in these two metrics. Much of this variability is due to the influence of elevation. As such, the river valleys, through which many of the primary transportation corridors of the state lie, exhibit a less severe frost penetration depth than the surrounding area. Elucidating this variability may be a useful discovery in terms of avoiding the cost of transporting non-native base course material for placement to unnecessary depths in new construction. Likewise, knowledge of this variability may now also result in the design of deeper pavement structures than previously assumed necessary at higher elevations.
This work was funded through the State Planning and Research program by the Federal Highway Administration and the Technical Planning Division of the Vermont State Agency of Transportation, Mike Pologruto, project manager.