2. Select the ROADs map:
3. Select the DEVELOPMENT map(s):
- (e.g., for 1990, and 2050)
4. Select the MATRIX QUALITY map(s):
- (e.g., National Land Cover dataset)
5. Select sensitivity to development and roads (matrix quality):
6. Specify minimum area required (in hectares)
-
- default "10, 50, 100" for the first time, otherwise defaults to values
that were run last time
7. Specify the edge threshold (0-100)
8. Specify the dispersal distance(s)
-
- default "10, 50, 100" for the first time, otherwise defaults to values
that were run last time
9. Comments
Output
The list of number of patches, and model parameters are written out to a tab-delimited text file that can be easily imported into Excel. The output GRIDs are added to a new view.
For each scenario run, a new view (named with a time-stamp) is
created and GRID output files are placed inside the view. Grids that begin
with "Patches
" provide output for patches of habitat that meet the
minimum requirements specified. GRIDs that begin with "Clusters
" provide
output for clusters of patches that are "connected" by dispersal ability and
matrix quality assumptions. Use the "Unique Value" legend to display, so
that same-colored patches are connected. Note that the GRIDs inside the
output view are "temporary" GRIDs, in the ArcView sense, so that they
physically located in the working directory. If you want to save these GRIDs,
make these permanent or copy them over into another directory that will not
get periodically cleaned.
Example of Lynx canadensis in the Southern Rocky Mountain Ecoregion
Note: the purpose of this example is to illustrate the modeling process in the
Southern Rocky Mountain Ecoregion (central Colorado, south-central
Wyoming, and north-central New Mexico), not to produce a definitive map of
lynx connectivity. Four major steps in the process are described.
The first step is to create the habitat map, and for the lynx in the Southern
Rocky Mountains I converted National Land Cover data to create a habitat
map (Figure 1). The 30 m resolution was aggregated to 300 m resolution
using BLOCKSTATS (with sum) to produce a GRID with values ranging from
0 to 100, or the proportion of a cell that is habitat. Using a coarser GRID
was needed to ensure that the cost-distance functions perform reasonably.
Based on housing density values, the effective area of habitat in a cell was
reduced (e.g., urban 100% loss, suburban 75% loss, exurban 50%
loss). Cells that had a highway run through them had a 100% loss of habitat
(while smaller roads had no reduction).

Figure 1. Creation of habitat map for Lynx in the Southern Rocky Mountain
Ecoregion. The coniferous and mixed forest cover types were extracted from the
USGS National Land Cover Dataset (30 m) represent, in a course way, critical
habitat for Lynx.
The second step is to determine habitat patches that meet the minimum
area requirement. Those patches that have an area smaller than A are
removed (Figure 2).

Figure 2. Removal of patches that are below the minimum area requirements.
Different color patches represent separate habitat patches, and patches that are to
be removed are shown in Red (Left) and subsequently removed (Right).
A third major step is to create the matrix quality map by reclassing the land cover map to reflect assumed resistance to movement (Figure 3). Resistance values are described in a reclass table (Table 1). Note that different assumptions about sensitivity of a species to movement through different types of land cover can be represented.
| Cover type | Low Sensitivity | High Sensitivity |
| Forest | 1.0 | 1.0 |
| Shrubland | 1.5 | 1.5 |
| Grasslands | 2.0 | 2.0 |
| Secondary roads | 2.0 | 2.5 |
| Ice-snow | 5.0 | 5.0 |
| Agriculture | 5.0 | 5.0 |
| Barren | 8.0 | 8.0 |
| Orchards-vineyards | 8.0 | 8.0 |
| Wetlands | 8.0 | 8.0 |
| Residential-Commercial | 10.0 | 100.0 |
| Highways | 20.0 | 1000.0 |
| Water | 100.0 | 1000.0 |

Figure 3. Conversion of land cover types to matrix quality. A resistance value for each cell is created through RECLASSing the land cover data (left) that has roads "burned-in". Higher resistance values are shown using darker shades of red (right), so that urban areas such as Denver (far right, top) and highways stand out.
The fourth step is to identify "clusters" of patches those that are within the
prescribed dispersal distance (Figure 4). That is, a single path between
patches is not assumed, rather, patches are found to be "connected" if any
part of a patch can reach any part of another patch assuming a given
dispersal distance (that reflects matrix quality). Using this methodology
provides much improved computer performance, as compared to finding the
least-cost path.
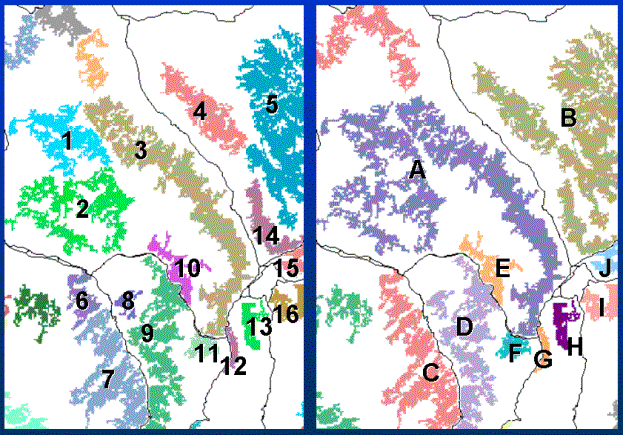
Figure 4. Finding "clusters of habitat patches. Individual patches are shown in unique colors (left).
Groups of patches that are within the dispersal distance are considered clusters.
For example, cluster "A" is composed of patches: 1, 2, and 3; "B" is composed of 4, 5, and 14; etc.
This modeling approach supports two modes of use. The first is that if
specific parameters are available for a given species, then those can be input
and the model results interpreted. But, a more robust mode of use is to
examine how connectivity changes over a range of parameter values (e.g., a
sensitivity analysis). The model input is set to handle this, as each set of
major parameters allows a list of parameter values. This enables a critical
range or threshold to be identified. For example, given a range of
sensitivities and dispersal ability, the output of a series of models can be
grouped to illustrate critical scales that might result in markedly different
connectivity regimes (Figure 5). The ability of a single species can be
compared directly to this critical scale. Also, a broad range of species can be
filtered to determine if they are likely to be sensitive to fragmentation.
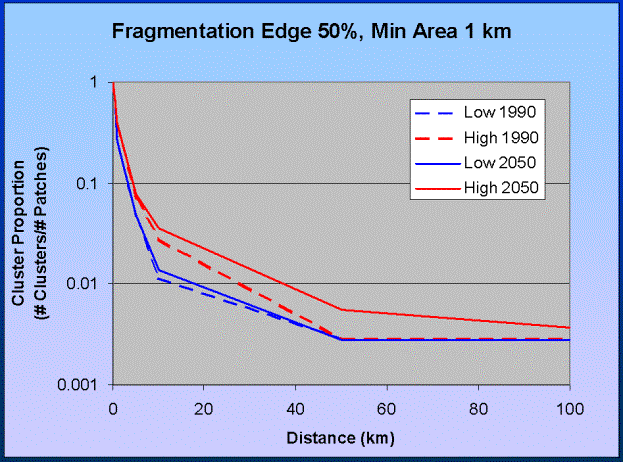
Figure 5. Identifying critical scales. A critical scale of dispersal ability occurs
between 10 and 30 km.
Also, by examining the output maps directly, locations on the landscape
that are critical to maintain connectivity can be identified (Figure 6). That is,
the "pinch-points" or "bottle-necks" to landscape movement can be readily
identified (Figure 7).
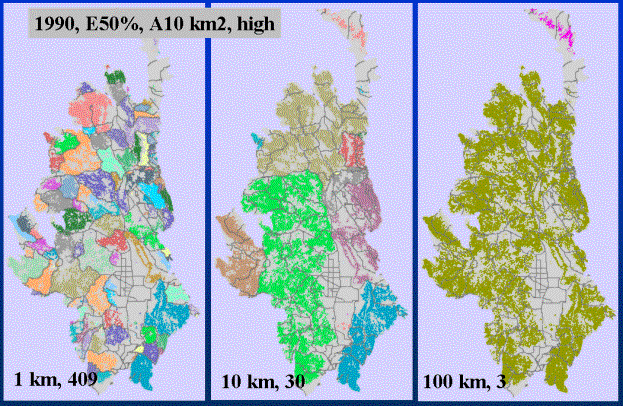
Figure 6. Dispersal ability ranging from 1 km to 10 km to 100 km. Different colored
areas represent distinct clusters of patches, so that at short dispersal distances
(Left), roads (grey lines) are seen to delimit patches and create a fragmented
landscape. With greater dispersal ability, landscape connectivity increases, and
important locations (I-70 west of Vail) become apparent (middle). At large
distances, the landscape is fairly-well connected.
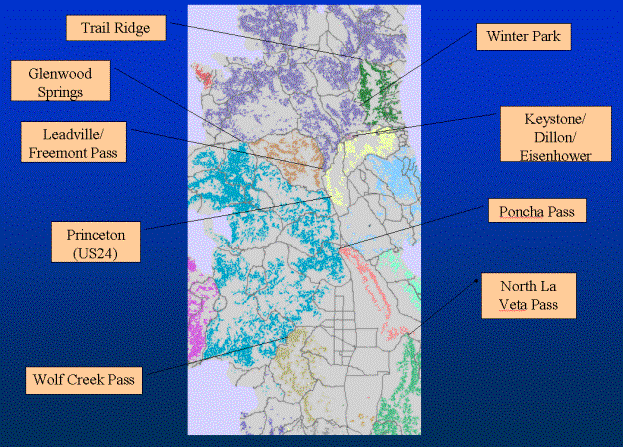
Figure 7. Pinch-points in the Southern Rocky Mountains for lynx.
Discussion
Because land use and roads are explicitly incorporated in the model, and alternative scenarios can be easily generated, fragmentation can be assessed in a meaningful way by comparing natural vegetation patterns to a human-modified landscape. Often, landscape fragmentation is being caused by modifications in the intervening matrix that are occurring at a much faster rate changes directly to the habitat. Given these situations, models of landscape fragmentation must incorporate direct changes to matrix. Ideally, model- and field-based inquiry operate in tandem. This modeling approach was developed to provide improved biological realism into understanding landscape-level processes, but models are typically challenged and rightly so -- on the basis of the empirical data that provide the foundation for the estimated input parameters. Modeling is valuable when field-based data are not available. An interesting finding of a model of black-bear dispersal near Banff, Canada (Clevenger et al. 2002) suggests that a model based on expert literature performed better, as assessed by comparison to an empirical model, than an expert opinion-based model. Also, models can be used to conduct a preliminary analysis to determine what field parameters are the most important to collect.
Landscape graphs
Most models have relied on the least-cost path to derive cost-distances between patches (e.g., Bunn et al. 2000; Singleton and Lehmkuhl 2000). Least-cost paths are presumed to better approximate the actual distance a species moves, as compared to Euclidean distance, but estimating these paths is demanding on computer resources (Bunn et al. 2000). Part of the demand is related to computing distances for all pairs of patches though assumptions of uni-directional flow require only roughly half of the pairs -- O(n(n-1)/2).
A refinement to this standard methodology uses "landscape graphs"
work in progress -- that differ from traditional graphs (sensu Bunn et al.
2000; Urban and Keitt 2001; Wallis 2000) in two ways. First, the topology of
landscape graphs is computed by establishing adjacencies through Thiessen
polygons (computed either with Euclidean- or cost-allocation methods).
Practically this reduces the number of edges (connections between nodes or
patches) in a graph and hence computation complexity -- and an adjacency
list stores only connected features (Theobald 2001). Second, instead of
computing inter-patch distance using the least-cost path, I find the average
distance of paths that travel through the shared boundary of the habitat
patches allocation polygon. Though this has not been tested, this more
reasonably approximates the approach of individual-based models that allow
for a probabilistic interpretation of species moving across a landscape (e.g.,
Boone and Hunter 1996; Shippers et al. 1996). The connection between
patches is represented, not as a straight-line edge between nodes, but as a
polyline that begins at a patch edge, passes through the mid-point of the
shared boundary of the Thiessen polygons, then ends at the adjacent patch
edge. This allows a somewhat more realistic portrayal of the linkage
between patches.
Acknowledgments
This work was completed with support from the David H. Smith Fellowship, The Nature Conservancy and the Colorado Department of Transportation. I thank Randy Boone for discussions about alternative approaches to least- cost path modeling.References
Addicot, J.F., J.M. Aho, M.F. Antolin, D.K. Padilla, J.S. Richardson, and D.A. Soluk. 1987. Ecological neighborhoods: scaling environmental patterns. OIKOS 49: 340-346.Boone, R. B. and M. L. Hunter. 1996. Using diffusion models to simulate the effects of land use on grizzly bear dispersal in the Rocky Mountains. Landscape Ecology 11(1): 51-64.
Bunn, A. G., D. L. Urban, and T. Keitt. 2000. Landscape connectivity: A conservation application of graph theory. Journal of Environmental Management 59(4): 265-278.
Clevenger, A. P., J. Wierzchowski, B. Chruszcz, and K. Gunson. 2002. GIS-generated, expert-based models for identifying wildlife habitat linkages and planning mitigation passages. Conservation Biology 16(2): 503-514.
Crooks, K. R. 2002. Relative sensitivities of mammalian carnivores to habitat fragmentation. Conservation Biology 16(2): 488-502.
Doak, D. F., P. C. Marino, and P. Kareiva. 1992. Spatial Scale Mediates the Influence of Habitat Fragmentation on Dispersal Success - Implications for Conservation. Theoretical Population Biology 41(3): 315-336.
Ferreras, P. 2001. Landscape structure and asymmetrical inter-patch connectivity in a metapopulation of the endangered Iberian lynx. Biological Conservation 100(1): 125-136.
Forman, R. T. T. and M. Godron. 1986. Landscape ecology, John Wiley & Sons.
Keitt, T.H., D.L. Urban, and B.T. Milne. 1997. Detecting critical scales in fragmented landscapes. Conservation Ecology [online]1(1): 4. URL: http://www.consecol.org/vol1/iss1/art4
Krist, F. J. and D. G. Brown. 1994. GIS modeling of paleo-indian period caribou migrations and viewsheds in northeastern lower Michigan. Photogrammetric Engineering & Remote Sensing 60: 1129-1137.
Moilanen, A. and M. Nieminen. 2002. Simple connectivity measures in spatial ecology. Ecology 83(4): 1131-1145.
Palomares, F., M. Delibes, P. Ferreras, J.M. Fedriani, J. Calzada, and E. Revilla. 2000. Iberian lynx in a fragmented landscape: Predispersal, dispersal, and postdispersal habitats. Conservation Biology 14(3): 809-818.
Paton, P. W. C. 1994. The Effect of Edge on Avian Nest Success - How Strong Is the Evidence. Conservation Biology 8(1): 17-26.
Ricketts, T. H. 2001. The matrix matters: Effective isolation in fragmented landscapes. American Naturalist 158(1): 87-99.
Schippers, P., J. Verboom, J.P. Knaapen, and R.C. Apeldoorn. 1996. Dispersal and habitat connectivity in complex heterogeneous landscapes: an analysis with a GIS-based random walk model. Ecography 19: 97-106.
Singleton, P. H. and J. F. Lehmkuhl. 2000. I-90 Snoqualmie Pass Wildlife Habitat Linkage Assessment, USDA Forest Service, Pacific Northwest Research Station, Wenatchee Forestry Sciences Lab. 69 pages.
Theobald, D.M. 2001. Topology revisited: Representing spatial relations. International Journal of Geographical Information Science 15(8):689- 705.
Theobald, D.M. and N. T. Hobbs. 2001. Functional definition of landscape structure using a gradient-based approach. In Predicting Plant and Animal Occurrences: Issues of Scale and Accuracy, edited by J.M. Scott, P.J. Heglund, M. Morrison, M. Raphael, J. Haufler, and B. Wall. Island Press, Covello, CA. Pgs. 667-672.
Tischendorf, L. and L. Fahrig. 2000. On the usage and measurement of landscape connectivity. OIKOS 90: 7-19.
Urban, D. and T. Keitt. 2001. Landscape connectivity: A graph-theoretic perspective. Ecology 82(5): 1205-1218.
Walker, R. and L. Craighead. 1997. Analyzing wildlife movement corridors in Montana using GIS. Proceedings of the Esri User Conference '97. http://gis.Esri.com/library/userconf/proc97/proc97/to150/pap116/p11 6.htm
Wallis, W. D. 2000. A Beginner's Guide to Graph Theory. Boston, MA, Birkhauser.
Wiens, J. A., N. C. Stenseth, B. Van Horne, R.A. Ims. 1993. Ecological Mechanisms and Landscape Ecology. OIKOS 66(3): 369-380.
With, K. A. and T. O. Crist. 1995. Critical Thresholds in Species Responses to Landscape Structure. Ecology 76(8): 2446-2459.
Author Information
David M. Theobald, Ph.D.David H. Smith Conservation Fellow, The Nature Conservancy
Research Scientist, Natural Resource Ecology Lab
Assistant Professor, Department of Natural Resource Recreation & Tourism
Colorado State University
Fort Collins, CO 80523-1499
davet@nrel.colostate.edu
970.491.5122