
An extended abstract
Regula Frauenfelder & Bernhard Schneider
Rockglaciers (Fig. 1) reflect debris accumulations produced, deposited and deformed during historical and Holocene time periods. They are efficient transport systems of frozen debris in the periglacial alpine environment, representing a process chain linking frost weathering, rock fall, and debris displacement by permafrost creep.

Figure 1: Examples of active Alpine rockglaciers: (left) Suvretta rockglacier in the Upper Engadin, Eastern Swiss Alps (photograph by R. Frauenfelder), (right) Marinet rock-glacier in the "Alpes Maritime", France (photograph by G. Lesueur).
Despite the growing number of rockglacier studies, knowledge and understanding with respect to the temporal and spatial variability of regional rockglacier occurrence is still rather limited. The aim of the presented study is, therefore, to test automatic methods for rockglacier detection at a regional scale.
The occurrence of rockglaciers is primarily limited by climatic preconditions. Furthermore, rockglaciers are found in areas characterised by specific topographic parameters: they occur within a certain altitudinal band (due to the prevailing mean annual air temperature), they favor certain expositions (due to differences in incoming radiation), they require a certain slope (flow of the ice-debris mixture must be possible) and they need a rock contributing headwall above them (ensuring continuing debris supply).
Geomorphometry, being the quantitative treatment of the morphology of landforms (cf. e.g. Evans 1972, Mark 1975, Pike 1995), builds upon the basic assumption that there exists a close relationship between surface processes and particular topographic characteristics, which themselves are expressed as topographic parameters. The presented study, thus, starts from the hypothesis that it is possible to detect potential zones of rockglacier occurrences with the help of geomorphometry, that is, from digital elevation models.
A rockglacier is composed – in a rough approximation – of a concave debris accumulation area and a convex creeping body (cf. Fig. 1). Both areas are connected by the root zone (RZ) where accumulated debris is susceptible to be triggered to creep. In our study we try to detect these rockglacier root zone areas.
Our study was conducted in the Upper Engadin, Eastern Swiss Alps, an area covering approximately 530 km2, stretching from 46°22’ N to 46°35’ N, and 9°39’ E to 9°59’ E. In this area, Hoelzle (1998) identified 84 active rockglaciers through field investigation and analysis of aerial photographs. Sixty-four of these rockglaciers originated most presumably as "classical" talus-derived rockglaciers. The other twenty rockglaciers developed in originally glacier-transported debris (mostly lateral and terminal moraines); this latter group will be labeled moraine-derived rockglaciers in the following.
The method applied is based on a hierarchical system for the extraction of geomorphometric parameters and objects presented by Schmidt & Dikau (1999). The system itself is based on the extraction of primary geomorphometric parameters. In a second step, these parameters are analysed to derive geomorphometric objects. These objects are the basis of a hierarchical system consisting of object analysis and object aggregation leading to representative geomorphometric parameters and geomophometric objects of a higher scale.
It is prerequisite to the detection to identify the geomorphic parameter that correlate well with the occurrence of the rockglacier root zones. We conduct three main working steps: firstly, we extract primary geomorphometric terrain parameters from the digital elevation model (DEM) of the study area. In a second step, we derive the statistical values (min, max, mean, and standard deviation) for each of these geomorphic parameters and compute classified parameter sets using the average, ± 0.5 standard deviation, and ± 1 standard deviation.
We then calculate the frequency distribution of each of these parameter sets with respect to the rockglacier root zones (RZ). These results are then plotted as histograms, which allows distinguishing parameters for which the root zones are evenly distributed i.e., parameters that are unfavorable for modeling from parameters showing an accumulation of root zones in distinct classes. In a third step, we then apply these parameters to derive the rockglacier root zones. Modeling results are directly compared with the empirically derived rockglacier root zones.
The geomorphometric parameters were derived from a DEM with 25 meters cell size. The geomorphometric analysis was carried out in ArcInfo, version 8.0.1, statistical parameters were calculated in KaleidaGraph, version 3.08d.
We use three different modeling approaches: (1) a combination of geomorphic parameters for all rock glaciers, (2) a geomorphic modeling approach for "classical" (talus-derived) rockglaciers only, and (3) a modeling procedure including rock fall accumulation areas.
(1) In a first run, we combine different sets of the geomorphometric parameters for all active rockglaciers (Fig. 2). The problems occurring in this approach are obvious: the amount of regions that are classified as potential rockglacier root zone areas without being characterised by rockglaciers in reality is very large. On the other hand, some rockglaciers that actually exist are not situated within the modeled zones of potential rockglacier areas, i.e. they are located in zones were they shouldn't be according to the model.

Figure 2: Approach 1: combination of the most significant geomorphometric parameters aspect, elevation, elevation-relief ratio, curvature, skewness, slope, relief and roughness for all active rockglaciers (marked with black lines). Higher saturated reds stand for higher likelihood of rockglacier root zones.
(2) In a second approach, we distinguish between "classical" talus-derived and moraine-derived rockglaciers (cf. above). We limit the geomorphometric analysis and the according detection to talus-derived rockglaciers. This allows us to exclude the effects of heterogeneity between the two groups of rockglaciers.
We then consider the range of occurring values of each parameter (e.g. active rockglaciers are found between 2230 m a.s.l. and 3500 m a.s.l.) and rule out the values outside this range.
Modeling with the resulting parameter sets (Fig. 3) allows for inclusion of all occurring talus-derived rockglaciers. However, the amount of areas that are falsely modeled as potential rockglacier areas, increases significantly compared to approach (1).

Figure 3: Approach 2: combination of the most significant geomorphometric parameters for talus-derived rockglaciers (black lines) using a procedure that considers the range of occurring values. Parameters used are aspect, elevation, wetness index, roughness, elevation-relief ratio, plan curvature, profile curvature, skewness, slope, and relief. The higher the red-color is saturated, the higher is the likelihood for the occurrence of rockglacier root zones, vice-versa indicate higher saturated blues lower likelihood for rockglacier root zones.
(3) In order to decrease the number of DEM cells classified as potential rockglacier areas, we limit the search to areas where rock debris supply is possible. To compute rock fall and rock fall accumulation, the so-called ‘overall-slope’ approach was used (Brändli, unpubl. 2001, Utelli 1999). Areas with slope angle equal to or greater than 40° are identified as rock debris sources, that is, as rock walls. A rock rolls along the steepest descent. It stops at the point where the straight line connecting the rock and its source point has a slope angle of 31°.
The inclusion of the rock fall areas led to a pronounced decrease in falsely modeled areas (Fig. 4). Yet, some problematic cases remain. They are basically of two kinds: (a) for very small (and often steep) rockglaciers the contributing headwall is not represented in a DEM with 25 meters resolution. Therefore, rock fall is not modeled in these areas. (b) Some rockglaciers do not exhibit a contributing headwall at all. The question why they are still active remains open, although it is likely that their activity will decrease, due to missing debris input.
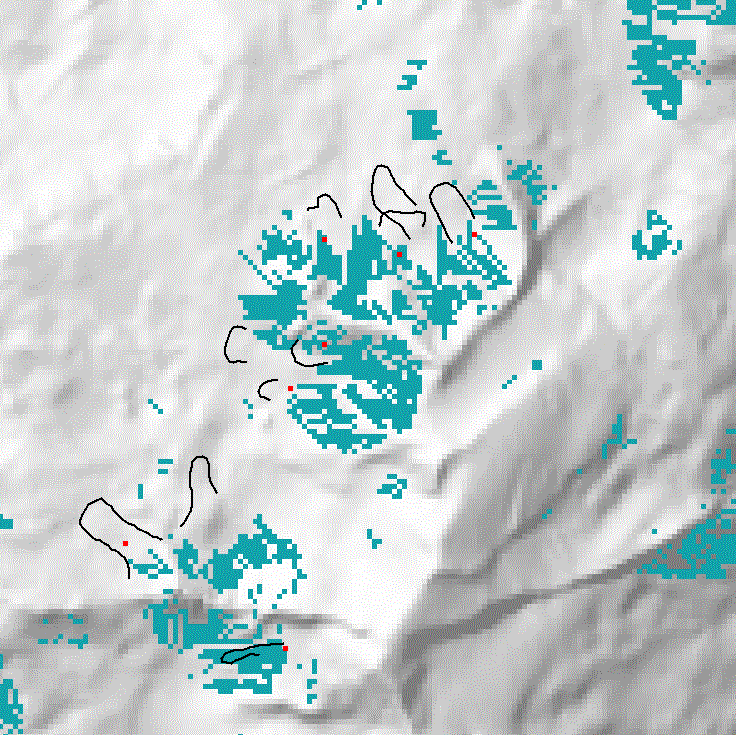
Figure 4: Approach 3: combination of the most significant geomorphometric parameters for talus-derived rockglaciers (black lines) using a procedure that considers the range of occurring values (cf. Approach 2), and including rock fall, i.e. zones were debris is actually available. Red points mark empirically derived rockglacier root zones (RZ).
Geomorphometry allows for a fast and relatively easy identification of areas theoretically suitable for rockglacier occurrences. However, a detailed modeling of the actually existing rockglaciers in a given area is not possible by the approaches applied.
There will always be the compromise between a modeling approach with unstinting boundary conditions, leading to large overestimation of the modeled rockglacier areas, and a modeling approach with narrow boundary conditions, leading to an increased number of objects (i.e. rockglaciers) that are not reproduced by the model.
Our results show that geomorphometry is an interesting method to delineate potential rockglacier areas on a larger scale, but that the main progress in rockglacier modeling must come from a process based approach concentrating on the physical parameters involved with permafrost creep (e.g. Olyphant 1983). The results of our study indicate that the consideration of rock fall proves to be one of the main prerequisites in such a model.
We are greatly indebted to Prof. Dr. Bernd Etzelmüller, University of Oslo, for having motivated the presented study. Further thanks are directed to Dr. Martin Hoelzle, without his spadework in putting together the rockglacier inventory, our work would not have been possible.
Evans IS. 1972. General geomorphometry, derivatives of altitude, and descriptive statistics. In RJ Chorley (ed.), Spatial analysis in geomorphology. Mathuen & Co Ltd, 17-92.
Hoelzle M. 1998. Rock Glaciers, Upper Engadin, Switzerland. International Permafrost Association, Data and Information Working Group, NSIDC, University of Colorado at Boulder. CD-ROM.
Mark DM. 1975. Geomorphometric parameters: a review and evaluation. Geografiska Annaler, 57A, 165-177.
Olyphant GA. 1983. Computer simulation of rock-glacier development under viscous and pseudoplastic flow. Geological Society of America Bulletin, 94, 499-505.
Pike RJ. 1995. Geomorphometry - process, practice and prospect. Zeitschrift für Geomorphologie, Supplement Band 101, 221-238.
Schmidt J, Dikau R. 1999. Extracting geomorphometric attributes and objects from digital elevation models – semantics, methods, future needs. In Dikau R, Saurer H. (eds.), 1999.
Utelli HH. 1999. Die Möglichkeiten von GIS bei der Beurteilung der Steinschlaggefahr im alpinen Bereich. Bulletin angewandte Geologie, 4, 3–18.
Regula Frauenfelder
Department of Geography
University of Zurich
Winterthurerstrasse 190
8057 Zurich, Switzerland
Dr. Bernhard Schneider
Department of Earth Sciences
University of Basel
Bernoullistr. 32
4056 Basel, Switzerland