The National Hydrography Dataset (NHD) is designed to facilitate studies involving a watershed of surface drainage. Each Catalog Unit of the NHD contains a drainage network that depicts the flow of surface water in a watershed. In the NHD, stream level refers to a numeric code that identifies a hierarchy for the main path of surface water through the drainage network. During the development of a higher resolution NHD, stream-level values must be updated to reflect the main paths of water through the more detailed drainage system. This paper describes an automated approach being used by the USGS to assign stream-level values during the production of the high-resolution NHD.
Any use of trade, product, or firm names is for descriptive purposes only and does not imply endorsement by the U.S. Government.
The National Hydrography Dataset (NHD) is a comprehensive vector representation of surface water features in the United States. Its development has been an ongoing effort among the U.S. Environmental Protection Agency (USEPA), the U.S. Geological Survey (USGS), and various other cooperating organizations. Being divided and distributed at watershed basin and subbasin (formerly called Catalog Unit or CU) boundaries, the NHD is designed to simplify environmental analyses that are affected by surface drainage.
Each subbasin of the NHD includes a drainage network of reaches where a reach is a significant segment of surface water that has similar hydrographic characteristics. Reaches are delineated between confluences in the drainage network, and each reach is assigned a unique and permanent address called a reach code. For a thorough explanation of the reach coding system, see "The National Hydrography Dataset: Contents and Concepts" ( USGS 2000).
A stream-level value is assigned to each reach in the drainage network. The stream-level value is a numeric code that identifies a hierarchy of main paths of water flow through the network. Level values are established for the purpose of computationally traversing the drainage network through flow relations identified between the reaches. Although the level-coding system appears to be the inverse of the Horton-Strahler stream-ordering system, it has not been determined that level values are correlated with the volume of water flowing through the network (Horton 1945, Strahler 1952).
At present, a complete version of the NHD is available at the 1:100,000 scale. This version was compiled from 1:100,000-scale USGS Digital Line Graph data. Although the 1:100,000-scale rendition of surface hydrography assists with regional environmental analyses, it does not provide the level of detail required for local analysis. Therefore, a higher resolution NHD is being generated at the 1:24,000 or larger scale. The generation of the higher resolution NHD includes a conflation process to maintain the lower resolution reach delineations and associated information, but because of mismatching linework between the two resolutions, some reaches must be redelineated or removed. Furthermore, there is much more detail in the high-resolution 1:24,000-scale version, and the stream-level values conflated from the medium-resolution NHD data may no longer be accurate. Additionally, the new streams added from the 1:24,000-scale data have not yet been assigned a stream-level value.
The remainder of this paper summarizes the stream-leveling process that is being implemented with the NHDCreate software, which is currently under development. This software is used for the generation of high-resolution NHD data at the USGS Mid-Continent Mapping Center. NHDCreate uses the geoprocessing functionality of Esri's ArcInfo Workstation and ArcView 3.2. It is implemented through Arc Macro Language (AML), Avenue, and C++ programming.
Stream level is assigned by identifying the terminus of a drainage network (see figure 1). The lowest value for stream level is assigned to a transport reach at the end of a flow and to upstream transport reaches that trace the main path of flow back to the head. The stream-level value is incremented by one and is assigned to all transport reaches that terminate at this path (that is, all tributaries to the path) and to all transport reaches that trace the main path of the flow along each tributary back to its head. The stream-level value is incremented again and is assigned to transport reaches that trace the main path of the tributaries to their heads. This process is continued until all transport reaches for which flow is encoded are assigned a stream level ( USGS 2000).
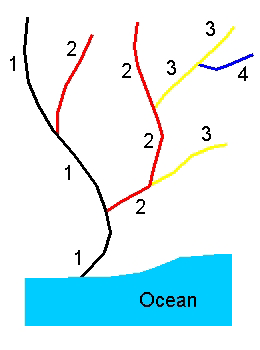
Figure 1. Stream-level assignment for a simple drainage network.
Initially, in the development of the high-resolution NHD stream-leveling tools, the same approach was taken that had been used for the medium-resolution data in determining the main path. Stream names were followed where possible, and the longest path was used to resolve the unnamed streams. Main paths were forced to follow stream names to more accurately select streams that had a higher likelihood of carrying the larger volume of water. The data were limited because they did not contain actual streamflow amounts. Therefore, the longest path might not always be the best choice for determining a main path. Using streams with the same geographic name was a good way to compensate for this limitation (see figure 2).
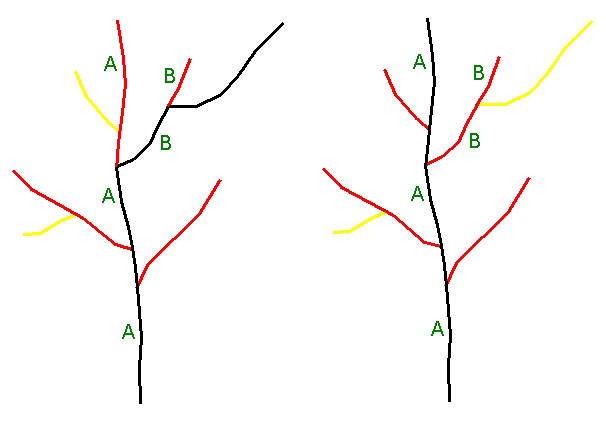
Figure 2. The first image depicts main paths selected by longest path alone. The second image depicts main paths selected through the use of both the longest path and the geographic name. The labels "A" and "B" represent the geographic stream names.
With the added detail of streams from the 1:24,000-scale data in the high-resolution NHD, an alternative leveling method is being utilized. It incorporates the arbolate sum value instead of the longest path in determining the main path. The arbolate sum is the sum of the lengths of all reaches upstream from the base of the immediate reach (USEPA 1996). In most cases, this value gives a better indication of the size of the drainage system upstream of the reach (see figure 3).
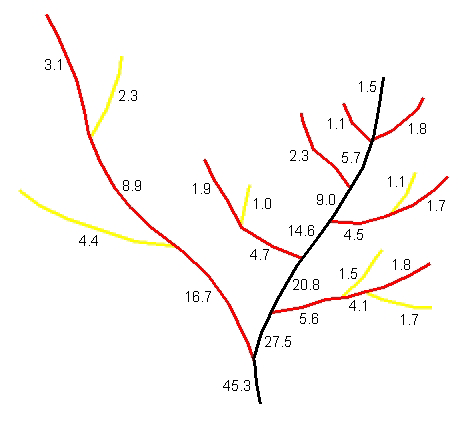
Figure 3. Arbolate sum values on a drainage network. Notice that the main branch to the right has a higher arbolate sum, but the branch on the left is actually longer.
There is one other factor that must be considered when leveling streams by individual subbasin. The main paths where the subbasins connect are not always chosen correctly, because the arbolate sum values from the subbasin upstream are not passed down to the subbasin below. To remedy this, a code is added manually to the subbasin data before the stream-leveling process is performed in order to identify these intersubbasin connections (formerly called inter-CU connections or ICC). This ICC code forces the leveling process to choose the proper main path where the arbolate sum value may indicate a different path (see figure 4).
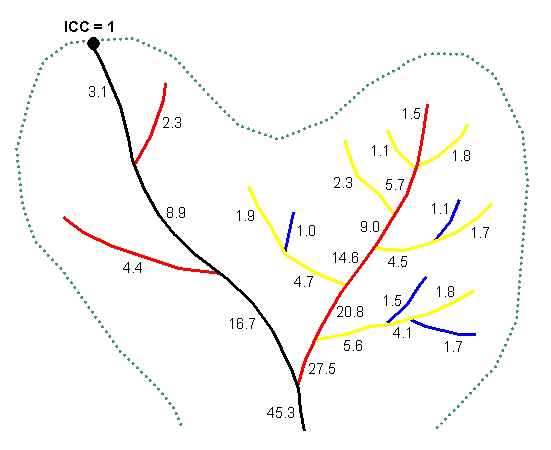
Figure 4. Main path forced to follow intersubbasin connection even though the arbolate sum of the main left branch is less than that of the right branch. The dashed line represents the subbasin boundary.
For stream-level processing, portions of the subbasin coverage's tabular data are output to text files using an AML. Then the AML calls the executable program that performs the actual stream-leveling task. The tabular data are then loaded into memory for processing. The stream network is treated like a standard tree structure and is traversed recursively using a depth-first search, starting at the point farthest downstream in the subbasin (Sahni 1998). An ICC code can be manually added to the data to force the program to start at a desired location. Otherwise, the starting point with the lowest existing stream-level value conflated from the medium-resolution NHD is used.
One complication arises when traversing the stream network in this manner. Braided streams, or what will be referred to as divergent areas, exist in the drainage system, which violate the basic properties of a normal tree structure. These divergent areas have branches that join back into each other, which means that there are multiple paths that lead from one point to another.
To overcome the problem of divergent areas, the idea of a link is introduced, which makes the data traversable like a standard tree structure. A link is just a symbolic connection between a stream flowing into the divergent area and the stream flowing out of it. This allows the program to jump over the complex area and wait to resolve it until later in the process. When a divergent area is encountered while tracing the drainage network upstream, a link is created for each stream flowing into the divergent area, connecting them to the out-flowing point. The link is treated just like a single stream, making the stream network appear to be a normal tree, thus allowing the depth-first search to continue at that point (see figure 5).

Figure 5. The first image depicts a simple divergent (braided) area. The second depicts the three links created for the three in-flowing streams. The links are represented by the dashed black lines.
The actual tracing algorithm used is difficult to explain without an indepth discussion about recursive programming, which is outside the scope of this paper. Basically, the network is traced upstream from the starting point. When an intersection is encountered, each stream branch at that intersection is traced arbitrarily, one at a time. If the tracing function reaches the end of a stream, it is assigned the minimum level value for the subbasin and returns its arbolate sum value, reach code, geographic name (if it has one), and ICC code (if it has one) back downstream to the previous intersection. Once all branches of the intersection have been traced, a decision is made as to which branch is the main path upstream from that point. The returned values from each branch are compared, and the main path is selected using the following order of precedence:
If any of the branches are links, and not actual streams, the levels for the streams inside the divergent area are resolved. This is accomplished by traversing the divergent area like a directed graph instead of a tree. The same order of precedence, as listed above, is used to find the main path, except that the shortest path is used in place of the greatest arbolate sum. The logic here is different because normally the main path through a braided stream area is the shortest path. After the main path has been determined, another function is called that traces the other branches upstream and increments the level of each by one. Then a new arbolate sum is computed and returned back to the next intersection downstream, along with the other return values listed previously. This process continues until the entire drainage network has been traversed and the tracing function returns back to the starting point.
Once the program returns back to the starting point, the stream-level processing is complete, and the new level values are output to a text file. These new levels are then joined to the subbasin coverage's attribute tables by the calling AML.
Stream-leveling results completed with NHDCreate were compiled to identify the percentage of reaches that were automatically assigned levels successfully. For testing, 13 subbasins were randomly selected that had already been assigned stream-level values and had been reviewed for correctness (see table 1). Looking at the results from all 13 subbasins, we see that the automated process shows about a 77.5 percent success rate. However, this program is still under development, and the problem causing the program to fail in two of the subbasins has been identified in the part of the code that handles divergent areas and is currently being corrected. The number of canal arcs are listed in the table because quite often subbasins containing a lot of canals have very large divergent areas, and the original algorithm used to handle these areas is displaying exponential complexity. This code is in the process of being rewritten using a much more efficient algorithm to eliminate the problem. Omitting the two subbasins that would not run because of this bug shows a success rate of 91.7 percent.
Most of the missed levels in the VA 6010205 subbasin were the result of one reach-level error, which caused the levels of all reaches upstream from that point to be off by one. This error is easily fixable using the QA/QC tools in NHDCreate. The program bug causing this error has also been identified and is being corrected. Also omitting the subbasin with the off-by-one error shows a success rate of 97.7 percent of reaches that were automatically leveled correctly. This is probably the most significant value because the errors that occurred in three of the subbasins are correctable problems in the program itself and not a major flaw in the overall automated stream-leveling process.
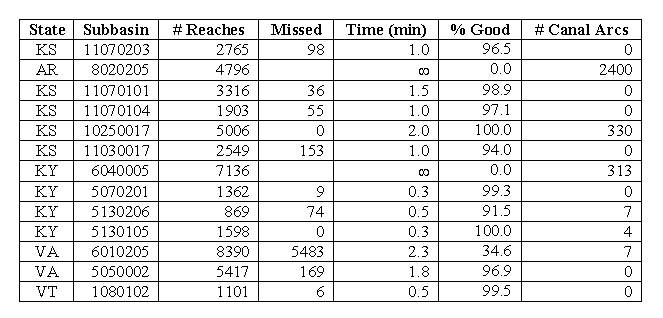
Table 1. Automated stream-leveling results. The ¥ symbol represents subbasins that failed to complete after 2 hours, and the program was manually halted.
Stream levels provide a valuable means to traverse the main paths of the surface water drainage network contained in the NHD. The stream-leveling process that has been integrated into the NHDCreate software has demonstrated that these levels can be automatically generated with a high degree of accuracy and a minimal amount of interactive editing. Once the identified corrections to the stream-leveling program have been completed, it is expected that at least 95 percent of the reaches in every subbasin of the high-resolution NHD can be automatically leveled. This is a substantial time savings compared with the length of time it would conceivably take to perform this process manually.
Even though the stream-level values generated are not based on actual streamflow, the arbolate sum with geographic name approach applied to the higher resolution NHD data appears to yield very good results. For future development, if actual streamflow data becomes available for the NHD, this process could be easily modified to use that information to provide even more accurate stream-level values.
Special thanks to all persons in the NHD section of the USGS Mid-Continent Mapping Center and Robbyn Abbitt of the Missouri Resource Assessment Partnership (MORAP) for their patient and vigilant software testing during the development of NHDCreate.
Horton, R.E. 1945. Erosional development of streams and their drainage basins: Hydrophysical approach to quantitative morphology. Geological Society of America Bulletin, 56, 275-370.
Sahni, Sartaj. 1998. Data Structures, Algorithms, and Applications in C++. Boston:McGraw-Hill.
Strahler, A.N. 1952. Dynamic basis of geomorphology. Geological Society of America Bulletin, 63, 923-938.
U.S. Environmental Protection Agency. 1996. USEPA Reach File Version 1.0 for the Conterminous United States. Accessed June 15, 2002, at URL http://www.epa.gov/owow/monitoring/rf/rf1_meta.html.
U.S. Geological Survey. 2000. The National Hydrography Dataset: Concepts and Contents. Accessed June 16, 2002, at URL http://nhd.usgs.gov/chapter1/index.html.