Federal legislation mandates that federal agencies must consider the impacts of their projects to historic properties, which include archaeological sites. Conducting an archaeological survey of every project and then determining whether a site is eligible for listing on the National Register of Historic Places is an expensive and time-consuming process. Mn/Model will be used as a planning tool by Mn/DOT and other agencies, allowing planners to avoid areas of high potential for sites. If avoidance is not possible it will allow for more efficient and cost-effective survey efforts by determining locations for intensive survey and areas where no survey may be required at all. By knowing in advance probable locations of significant archaeological properties, Mn/DOT will avoid impacting these non-renewable resources. This paper focuses on the development of the model and some preliminary results.
However, we also know that these key resources, their locations, and the landscapes containing them have changed through time. We have to use the information we have about today's landscapes and the very limited information we have about past landscapes to identify the spatial relationships between known archaeological sites and key resources.
Data from other raster sources is being regridded to the 30 meter cell size. Vector data from a range of source scales is being converted to raster. There is some concern about the possibility of making erroneous correlations with data that are more coarse, therefore less "accurate". However, given the scarcity of high resolution data available, we are using the best data we can find and attempting to account for varied resolutions when interpreting our results.
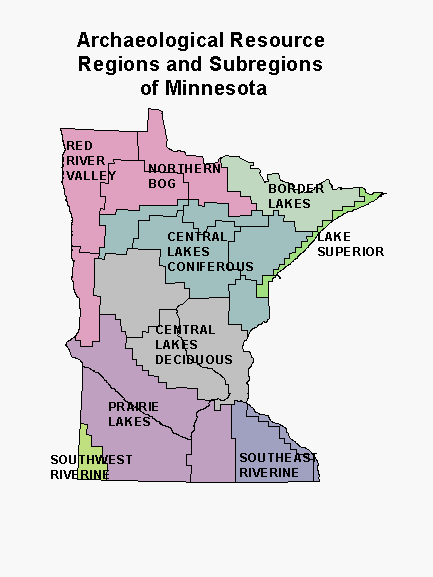Because of the variation in climate, vegetation, and topography across the state, our basic geographic units for modeling are nine archaeological resource regions and 21 subregions. These were defined by Scott Anfinson (Anfinson, 1990), archaeologist at the State Historic Preservation Office, based primarily on characteristics of the surface hydrology.
Essentially, the statewide model is really a mosaic of a number of different models. We have unique models for each region, and some subregions. Within each region and subregion, we may also have a mosaic of models, as we have data from some counties that are not available for others. For instance, if we find that high resolution soils data improves a model in a particular region, we can apply the improved model only to the counties in that region that have digital soil maps.
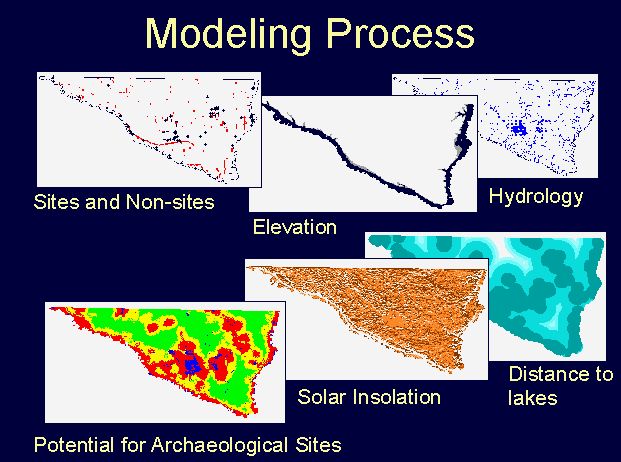The development of the model goes through several distinct stages. The first is data conversion, followed by deriving environmental variables from the data. The final stage is analyzing and evaluating the relationship between the archaeological database (the dependent variable) and the environmental (or independent) variables.
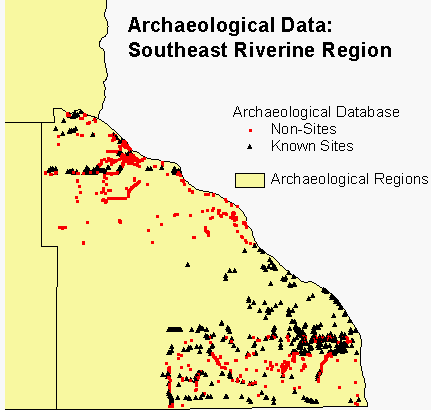The archaeological data consist of known archaeological sites from the files of the State Historic Preservation Office and random points located in areas that have been surveyed, but where no archaeological sites were found. For several counties we also received site data from the US Forest Service and the US Park Service. For our second phase of modeling, we generated additional random points using GRID. The random points are essential for building the model. We assume that the population of known sites will be found only in certain kinds of environments, whereas the random points can be found in any environment.
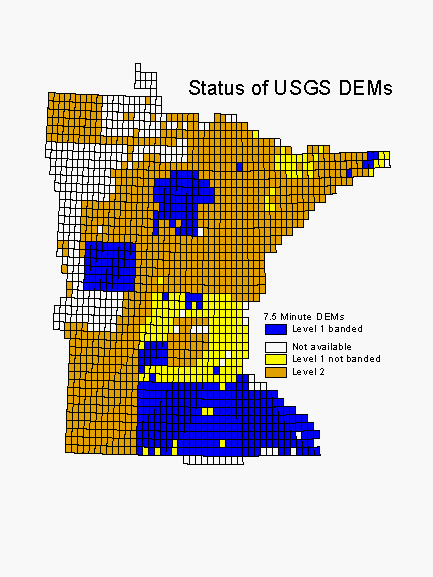Elevation and hydrology are our two most important environmental layers. Elevation is being derived from 7.5 minute DEMs. These are of varying quality and availability across the state. Banding, a north-south or east-west distortion in the data, is present on a number of the Level 1 DEMs. Where banding is present, we apply a filter to the data before deriving aspect or solar insolation. Where 7.5 minute DEMs are missing, we substitute (and regrid) 1:250,000 DEMs.
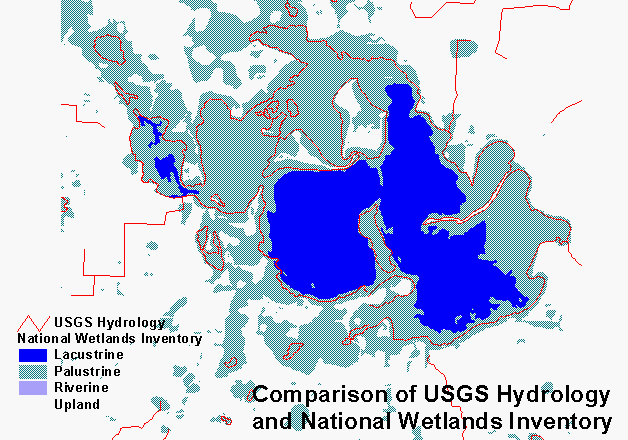We are taking lakes, double line rivers, and wetlands from the National Wetlands Inventory, which is complete in digital format for the entire state. Perennial and intermittent streams are from the Mn/DOT Base Map, which was digitized from USGS 7.5 minute topographic maps. Because the base map features have not yet been built and attributed as polygons, we could not use the lakes and double line rivers from that source. There is clearly a difference in how lakes and wetlands are interpreted between these two sources. We do not know how that will affect the model, but this should be investigated when the base map is ready to be treated as polygons.
We are also using a statewide raster database for data layers derived from the State Soil Atlas (original resolution 40 acres), a digitized 1:500,000 map of presettlement vegetation (Marschner, 1974), digital soils data from county soil surveys where they are available, and several other layers.
Once the raw data layers are converted, we then use them to derive the environmental variables. Derived variables include such things as distances to key resources and terrain characteristics like slope or roughness. For instance, solar insolation calculated from elevation data provides information about micro-climate, essentially indicating which places in the landscape are warmer in winter or cool and shady in summer. We have experimented with more than 100 variables over the course of the project. Many of these have been discarded for a variety of reasons: they may be redundant with other variables, they may be at an inappropriate scale, they may show no relationship to archaeological sites in the preliminary analysis. We make a distinction between variables derived from data that are available statewide and those that are available only for certain regions or counties. Our basic models use only variables that can be applied statewide. After basic modeling is complete, we will develop enhanced models for selected areas using variables derived from data that are available only regionally or locally. We are currently working with a list of 69 variables that are available for every county and several more that are available for only certain counties. Fewer than half of these have figured into models.
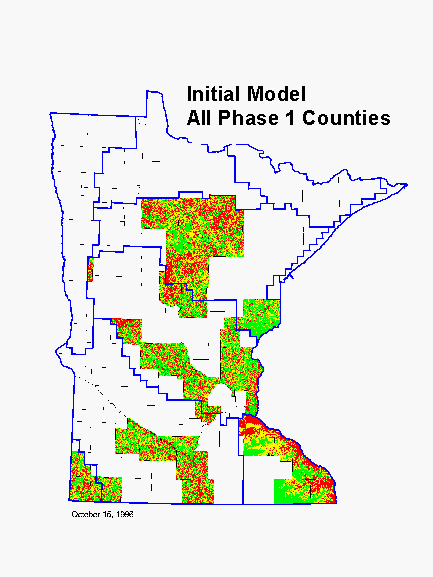We first modeled only the regions that contained Phase I counties. These models were based only on Phase I county data, which was our highest quality archaeological survey data. A mosaic of these models became our Initial Model. It was applied only to Phase I counties because data for Phase II counties were still being converted. The green areas are low probability for archaeological sites, the yellow areas are medium probability, and the red areas are high probability.
When Phase II data conversion was complete, we applied our initial models to the Phase II counties and evaluated their performance. Finally, we refined our modeling methods and developed completely new models incorporating site data from both Phase I and Phase II counties. The later models in some cases were developed for subregions, rather than for regions. Also, several data layers that were not available when the Phase I models were developed were used to build the Phase II models.
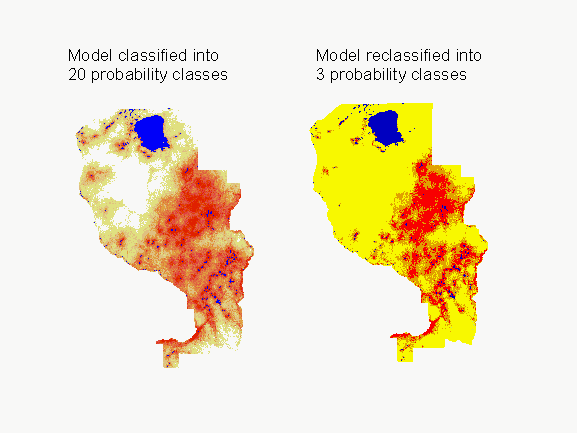Applying the logistic regression model produces a grid of values between zero and one, indicating the probability of finding an archaeological site in each cell. Our initial models were sliced into three equal-area probability classes (high, medium, and low probability), and we evaluated the models on the basis of the number of known sites found in each class. To reduce the size of the high and medium probability areas, we now slice models into 20 equal area probability classes, after first excluding water bodies, surface mines, and steep slopes. We then determine the number of known archaeological sites in each probability class. On the basis of this information, we reclassify the model into three classes (high, medium, and low probability) based on the following criteria:
1. Approximately 70% of known archaeological sites should be in the high probability area.
2. An additional 15% of known archaeological sites should be in the medium probability area.
3. The remaining 30% of known archaeological sites should be in the low probability area.
Our goal is to have the high and medium probability areas (red and orange on the model maps) occupy as little of the landscape as possible, while still containing approximately 85% of known archaeological sites. We assume that, if our model performed no better than chance, the high probability area containing 70% of the sites would occupy 70% of the area mapped. Likewise the medium probability area would occupy 15% of the landscape and the low probability area the remaining 30%. On the other hand, a good model would have a large percentage of known sites occurring in a small percentage of the landscape.
Theoretically, the proportions of sites within each probability class are set by our classification criteria and only the area in each class should vary. However, large clusters of sites within a small range of model values often prevent having 70% of the sites within high or 85% within high and medium categories. For this reason both proportions of sites and areas of each probability class vary between models. Given these conditions, Kvamme's Gain Statistic (Kvamme, 1988) is useful for evaluating model performance and comparing different models. It is calculated as (1 - % area / % sites). Values range from 0 to 1, with higher values indicating better performance. For instance, if 70% of the sites are in 15% of the area, the gain statistic would be 0.79. However, if 70% of the sites are in 30% of the area, the gain statistic would be only 0.57. By chance, 70% of the sites would be expected to be in 70% of the area, producing a gain of 0.
All of the models presented here were developed from basic variables, i.e. those that are available from statewide databases, and apply to all types of archaeological sites except single artifacts (isolated finds). Single artifacts were excluded from modeling because it is assumed that they could occur anywhere in the landscape, whereas concentrations of artifacts indicate longer occupation and will be more selectively located.
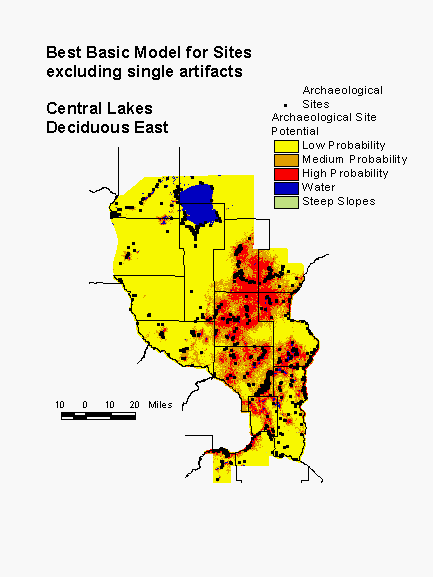The model for this subregion is based on a number of vegetation, terrain, and distance to water variables. The large scale pattern of the model, that of a concentration of high probability areas in the southeastern portion of the region, corresponds fairly well to the distribution of hardwoods. The vegetation variables used to calculate the model are distance to aspen/birch woodland, distance to pine barrens, distance to river bottom forest, and distance to mixed forest. The more local variation is a function of terrain (relative elevation, slope, surface roughness, and height above surroundings) and both present and past hydrology (distance to nearest large lake, distance to permanent lake, direction to permanent water, distance to large rivers, distance to glacial lake sediment, distance to perennial lake inlets/outlets, distance to river confluences, and direction to water and wetlands). Direction to water bodies is thought to be important because of the prevalence of fires, which usually move through the region from the southwest. Being on the east side of water bodies would provide some protection. This model places 81% of known sites in high and medium probability areas, which constitute 33% of the landscape.
The strong influences of vegetation variables in this model suggest that the subregion is poorly defined, since about half of it was originally dominated by coniferous forest. The current model probably overestimates the extent of high probability areas in the deciduous forest area and underestimates the area of high probability in the coniferous forest area. Redefining the region, by putting the northwest half into the adjacent Central Lakes Coniferous Region and combining the southern half with Central Lakes Deciduous South, would probably improve our ability to model both coniferous and deciduous forest areas.
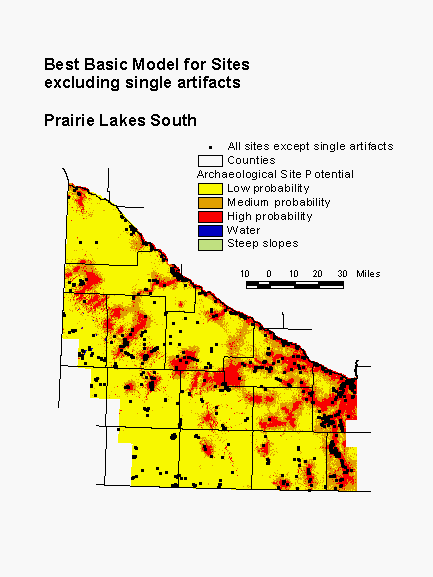The Prairie Lakes Region occupies a large part of the southern half of Minnesota. It is dominated by prairie, with many lakes and wetlands. The Minnesota River Valley, which bisects the region, is deeply incised, while the uplands are relatively flat. The model for the Prairie Lakes South subregion indicates the importance of water, wood, and terrain. Proximity to present and former water bodies is represented in the model by the variables distance to nearest permanent lake, distance to areas of organic soil, and distance to nearest perennial lake inlet/outlet. Wooded land is scarce in this subregion. Distance to hardwoods, which would be concentrated near water bodies, is a variable in this model. Finally, height above surroundings and relative elevation indicate the importance of local high spots for site location. This model places 81% of known sites in high and medium probability areas, which constitute 34% of the landscape.
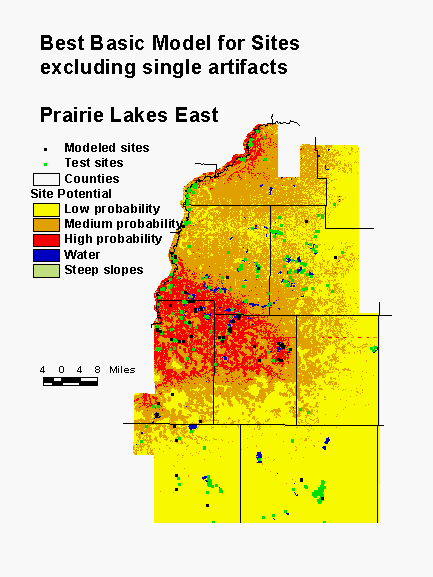The model for the adjacent Prairie Lakes East subregion provides another example of poor region definition. The northwestern part of the subregion was not prairie, but was dominated by deciduous forest. Most of the high and medium probability areas are concentrated in this region. Distance to edge of nearest water, distance to paper birch, distance to Kentucky coffee tree, and height above surroundings are the variables in the model. Both Kentucky coffee tree and paper birch were important species for hunter gatherers. It may be true that sites are more likely to be found near these species or in the deciduous forest in general. However, sites are found on the prairies as well, and these are not accounted for in this model.
This is because problem of combining two dominant vegetation types in one region is compounded by very different distributions of the sites used to build the model and the sites used to test the model. Most modeled sites are concentrated in the area dominated by deciduous forest in the presettlement period. However, the majority of sites in the subregion are in the test population and these are distributed throughout the region, much of which was prairie. Consequently, though the model predicts the population of modeled sites very well, it does a poor job of predicting the test population. In this model, only 66% of the sites are in the high and medium probability areas, which constitute a full 43% of the landscape. Redefining the regional boundaries would undoubtedly improve our ability to model this area.
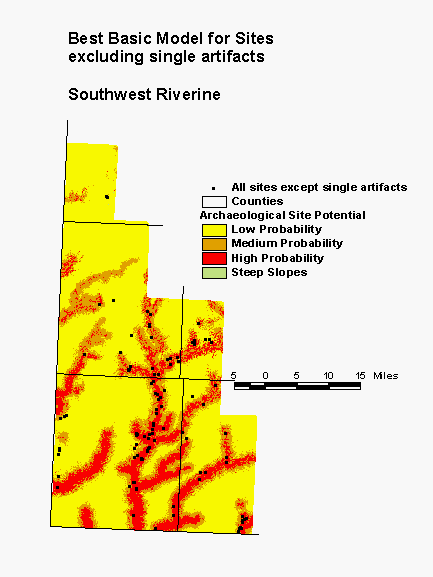In the southwestern corner of the state, the Southwest Riverine Region is dominated by prairie, interrupted only along the drainages of several large streams. Large lakes are not present, but small lakes do occur along some of the streams. Although the model for this region clearly picks up the dendritic pattern of the stream drainages, the streams themselves do not figure into its calculation. Only the distance to perennial lake inlets/outlets contains information about water. However, several of the drainages that are prominent on the model map do not contain lakes. Apparently the two terrain variables in the model, surface roughness and height above surroundings, are capable of distinguishing stream valleys from uplands. In this model, 86% of the known sites are in high and medium probability areas, which constitute 35% of the landscape.
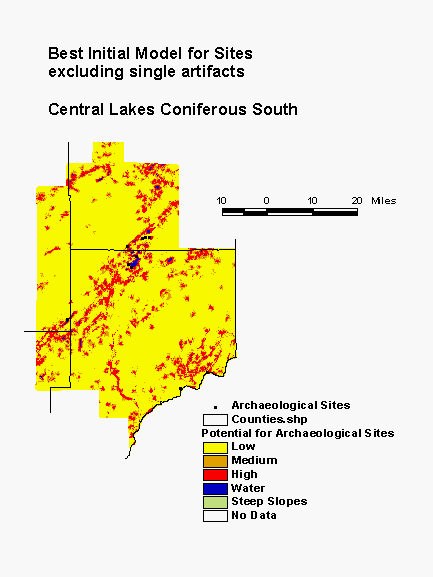The Central Lakes Coniferous Region is in glaciated terrain, pockmarked with lakes and wetlands and covered primarily with coniferous forest. Archaeological sites are rather sparse. The best initial model for the region was built using the same variable selection techniques as the more recent models presented above, but with fewer variables input. Vegetation variables were not considered in the development of this model. Nevertheless, it performs well. A combination of water bodies and terrain are the best predictors of sites in this region, including distance to nearest lake, distance to nearest perennial river, vertical distance to permanent water, and relative elevation.
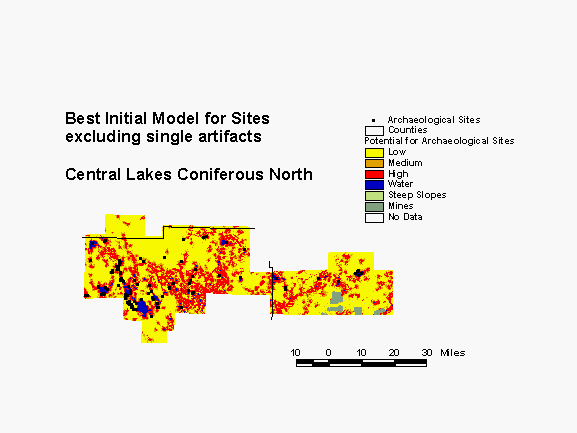In the southern portion of this region, the model places 91% of all known sites within the high and medium probability areas, which constitute 35% of the landscape. In the northern part of the region, only 85% of known sites are in high and medium probability areas, which constitute 39% of the landscape. The gain statistic in the south is 0.62, compared to only 0.54 for the north. The gain statistic for high probability areas alone in the south is 0.76; in the north it is only 0.67. Thus, this model performs as well as more recent basic models only in the southern subregion. When new models are developed for this region, they will consider more variables, including vegetation. Also, new models will be developed for subregions rather than the entire region. This should allow the models to better represent the environmental diversity across this large portion of the state.
For more information about the Mn/Model Project, visit the Minnesota SHPO home page. More information about the Mn/Model project
Kohler, T.A. and S.C. Parker, 1986. 'Predictive models for archaeological resource location'. Advances in Archaeological Method and Theory, vol. 9, pp. 397-452. (Academic Press, Inc.).
Kvamme, Kenneth L. 1988. 'Development and testing of quantitative models.' In Quantifying the Present and Predicting the Past: Theory, Method, and Application of Archaeological Predictive Modeling, edited by W. James Judge and Lynne Sebastian, U.S. Department of the Interior, Bureau of Land Management, Denver, CO. pp. 325-428.
Kvamme, Kenneth L. 1992. 'A predictive site location model on the High Plains: an example with an independent test.' Plains Anthropologist 37(138): 19-38.
Marschner, F. J. 1974. The Original Vegetation of Minnesota (map). Compiled from U.S. General Land Office Survey notes. North Central Forest Experiment Station, Forest Service, U.S. Department of Agriculture, Folwell Avenue, St. Paul, Minnesota 55101. Redrafted from the original by Patricia J. Burwell and Sandra J. Haas, Cartographers, University of Minnesota, Department of Geography, under the direction of Miron L. Heinselman, Principal Plant Ecologist.
Warren, Robert E. and David L. Asch. 1996. A predictive model of archaeological site location in the eastern Prairie Peninsula, Illinois. Illinois State Museum, Springfield, Illinois.