Pin-Shuo Liu and Yue-Hong Chou
Each year, wildfires cause tremendous loss of natural resources, endangered species, human lives and property. A better understanding of the direction, location, rate of spread, intensity, and burned areas of wildfires is important for both long-term wildfire management planning and effective suppression strategies.
This research provides a cell automation method to simulate wildfire propagation over spatial and temporal variability by using a grid-based GIS. Fire growth direction and location are simulated based on the probability value of fire occurrence of each grid cell. A spatial model of fire occurrence probability (Chou 1991, 1992, 1993, Chou et al. 1990, 1993) has been created to estimate the distribution of fire occurrence probability in the Bee Canyon of San Jacinto Mountain where a major fire occurred in 1996. A grid automation model extrapolates the eight neighboring cells from each burning cell by comparing the adjusted probability value of fire occurrence with a computer generated random number. Rothermel's model was employed to estimate the rate of spread and fire intensity. The simulated pattern of fire growth was compared to the empirical distribution of fire propagation. The results indicate that the cell automation method provides useful information for management of wildfires over a heterogeneous landscape.
Each year, wildfires cause tremendous loss of natural resources, endangered species, human lives and property. Between Oct. 26, 1993 and Nov. 4, 1993, for example, more than a dozen wildfires raged in six southern California counties. Wildfires swept over 200,000 acres of land, destroyed 1,000 homes, and the damage by these fires was estimated at 950 million dollars (Facts on File 1993). In January 1994, more than 150 bush fires ravaged cities along the 750-mile eastern coastline of the Australian state of New South Wales. These fires spread over 1.9 million acres of land, destroyed thousands of homes, and cost between 50 million and 100 million Australian dollars (Facts on File 1994). The ability to understand and predict wildfire intensity, direction, location, rate of spread, and burned area is important for effective wildfire management and suppression. Information regarding where a fire spreads, when the fire will reach a certain location, fire intensity, and the rate of spread is crucial for wildfire management. Different fire characteristics call for different containment plans, such as: active containment, selective suppression, or controlled burning.
If fire growth behavior can be predicted more precisely, then the destruction wrought by wildfires can be limited. Better prediction of the pattern and intensity of fires will help the control method and arrangement of suppression forces.
Fire behavior is a product of the environment, and is determined by topography, fuel, weather, and fire itself. In (Figure 1), the fire environment triangle shows the interaction between those environment factors which make up the fire environment. The changes of each environmental component will interact with other components and will lead to the changes of fire characteristics. This research considering topology, fuel, and weather variables to develop a GIS grid automation method to predict wildfire propagation across both time and space.
GIS technology offers opportunities to expand existing fire models to encompass vegetative and topographic heterogeneity over time. The complexity of fire behavior is due to the wide range of fuel characteristics and environmental conditions that determine the dynamics of fire behavior. In this research, we created a spatial database that includes multiple layers of fuel type, meteorological conditions, and topological characteristics. This study uses ArcInfo GIS for organizing, retrieving, processing, and displaying spatial data. In wildfire management, users can quickly find answers by using different query techniques implemented in a GIS. Before a fire occurs, the GIS can be used to inventory the conditions of the management area, model the probability of fire occurrence, estimate the damage, and manage the evacuation and extinguishment planning. Even during a burn, the GIS can be used to help predict the areas that are most likely to burn and identify the damaged areas, prepare updated maps showing such critical areas and their attributes, and respond to particular queries. After the fire, the GIS is useful for inventorying the damage and manage the recovery plan.
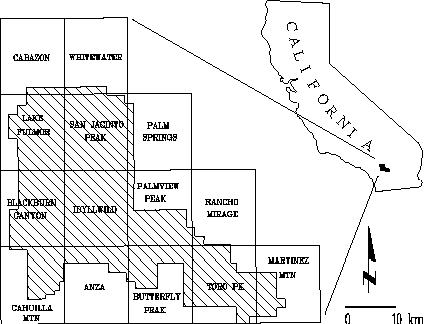
The San Jacinto Ranger District of the San Bernardino National Forest (Figure 2) is located 150 km east of Los Angeles, California. This area is dominated by the Mediterranean climate, which has hot, dry summers and cool, wet winters. The San Jacinto Mountains are surrounded by deserts. Precipitation increases with elevation from 30 cm at Hemet to 70 cm along the crest of the range, then decreases to 10 cm in the deserts. The major precipitation is due to prevailing northwestern frontal systems approaching from the Gulf of Alaska. Tropical thunderstorms sometimes occur in July and August (Minnich 1986).

Figure 2. The San Jacinto Ranger District, San Bernardino National Forest, California (Chou 1993).
The database is organized into 14 USGS 7.5-min topographic quadrangles. A well recorded history of fire activity provides the data necessary to construct probability models of fire occurrence. Data layers have been established in this study include fuel, slope, aspect, wind direction, wind speed, fire activity, temperature, precipitation, man made structures, roads, and river systems.
Vegetation is classified into eight major categories: wet meadow, open pine, dense chaparral, open chaparral, firs, oaks, water, and bare ground. These eight major categories is reclassified into thirteen BEHAVE standard fuel models by comparing the vegetation with photo guides (Anderson, 1982). The fuel models are sets of numerical values describing a fuel type, and are used in a mathematical model for predicting spread rate and intensity (Rothermel 1972). The slope and aspect data are obtained from digital elevation models (DEM) for the 14 quadrangles (U.S. Geological Survey 1987). Using the ArcInfo GIS (Environmental Systems Research Institute 1987), digital elevation can be converted into a coverage of homogeneous surface units called triangulated irregular networks. Aspect is then measured in degrees and slope is measured in percentage. In the fire history coverage, the areas in which major fires occurred between 1911 and 1984 (file data, San Bernardino National Forest) were digitized into polygons coded by burn year.
By applying temperature, precipitation, man-made
structures, fire history, vegetation, and transportation data
layers and analyzing spatial autocorrelation relationships, a
probability model of fire occurrence was constructed using Logistic
regression models (Chou 1991, 1992, 1993, Chou et al. 1990, 1993).
Logistic models are based on a sample of n independent
observations and each observation is described by p independent
variables. The dependent variable 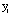 is linked
to the independent variables through the logistic function (Wrigley
1976, Chou 1991,1992) such that:
is linked
to the independent variables through the logistic function (Wrigley
1976, Chou 1991,1992) such that:
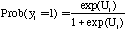
where 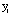 denotes the value of
the dependent variable for the
denotes the value of
the dependent variable for the 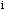 th observation
(
th observation
(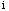 = 1,2,3,4,,,,n).
= 1,2,3,4,,,,n). 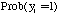 denotes the probability for the ith polygon to burn.
denotes the probability for the ith polygon to burn. 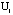 is a vector product of the form:
is a vector product of the form:
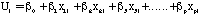
where 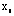 denotes the value of
the j th independent variable (j = 1,2,3,....,p
) for the i th observation.
denotes the value of
the j th independent variable (j = 1,2,3,....,p
) for the i th observation. 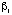 denotes
the value of the coefficient. The probability for the i th
polygon to burn is determined by the quantity
denotes
the value of the coefficient. The probability for the i th
polygon to burn is determined by the quantity 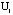 which has a value between zero and unity. A greater
which has a value between zero and unity. A greater 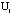 implies a higher probability for a fire to occur in the polygon.
implies a higher probability for a fire to occur in the polygon.
The probability for an area to burn has no direct relationship to the probability of ignition because not all ignitions develop into major wildfires. Some fires may die down on their own due to lack of fuel while others may suppress quickly. Therefore, for an ignition to develop into a major fire, there must be certain human, environmental, and spatial factors that favor the spread of the fire.
Neighborhood effects play an important role in the distribution of wildfire, and the forecasting accuracy of the logistic regression model of wildfires is improved significantly by incorporating the spatial term of contiguity (Chou 1991, Chou et al. 1990, 1993). In this study, the degree to which wildfires are spatially autocorrelated is tested using Moran's I coefficient (Moran 1948, 1950), such that
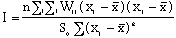
where n is the number of polygons delineated in the
coverage. 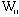 is a measure of the contiguity
between polygon
is a measure of the contiguity
between polygon 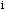 and polygon
and polygon 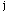 .
If the value of I is equal to 1,
.
If the value of I is equal to 1, 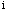 and
and
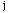 are contiguous; if the value is equal
to 0,
are contiguous; if the value is equal
to 0, 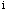 and
and 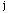 are
not contiguous.
are
not contiguous. 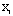 equals 1 if the i
th polygon was burned and otherwise equals 0.
equals 1 if the i
th polygon was burned and otherwise equals 0. 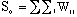 is the total number of neighboring pairs.
is the total number of neighboring pairs.
A FORTRAN computer program was developed to derive Moran's I and the related statistics for significance testing directly from the attribute tables in the database. Therefore, this model includes the structural, environmental, and spatial factors, such that:
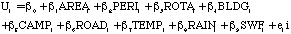
where 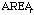 denotes the area of
denotes the area of
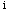 th polygon;
th polygon; 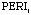 is
its perimeter;
is
its perimeter;  is the fire rotation weight
defined by vegetation in table 1;
is the fire rotation weight
defined by vegetation in table 1; 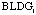 ,
, 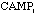 ,
and
,
and 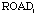 are the distance of the
are the distance of the 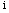 th
polygon within the range of significant human influence based
on buildings campgrounds, and roads, respectively;
th
polygon within the range of significant human influence based
on buildings campgrounds, and roads, respectively; 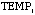 and
and 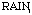 denote the average July-maximum temperature
and annual precipitation;
denote the average July-maximum temperature
and annual precipitation;  represented
the spatial term of neighborhood effects; and
represented
the spatial term of neighborhood effects; and 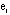 is the random error term.
is the random error term.
Table 1. Fire rotation weight defined by vegetation
| Vegetation Class | Rotation Period | Rotation Weight |
| ________________________________________________________________ | ||
| Bare Ground | Infinity | 0.0 |
| Water | Infinity | 0.0 |
| Wet Meadow | 100 years | 0.5 |
| Open Pine | 50 years | 1.0 |
| Chaparral (dense) | 50 years | 1.0 |
| Chaparral (open) | 200 years | 0.25 |
| Firs | 50 years | 1.0 |
| Oaks | 50 years | 1.0 |
Coefficients of the parameters are estimated from the stepwise logistic regression program (LR) in BMDP (BMDP P-series, 1987). Table 2 shows the results of the model.
Table 2. Statistics of the model
| ___________________________________ | ||
| Parameter | 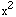 | p-Value |
| ___________________________________ | ||
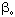 | 37.9 | 0.0000 |
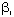 (AREA) (AREA) | 0.74 | 0.3894 |
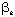 (PERI) (PERI) | 0.76 | 0.3824 |
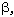 (ROTA) (ROTA) | 13.65 | 0.0002 |
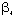 (BLDG) (BLDG) | 1.33 | 0.2483 |
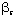 (CAMP) (CAMP) | 0.00 | 0.9690 |
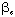 (ROAD) (ROAD) | 2.66 | 0.1026 |
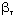 (TEMP) (TEMP) | 10.25 | 0.0014 |
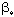 (RAIN) (RAIN) | 0.12 | 0.7264 |
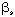 (SWF) (SWF) | 9337.4 | 0.0000 |
Log Likelihood = -121.979
_______________________________________________
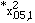 = 10.247
= 10.247
Among the explanatory variables in the basic model,
the spatial term generates the highest level of 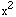 statistic.
Other variables of statistical significance at 0.05 level include
fire rotation and July maximum temperature. This model can be
expressed as the following form:
statistic.
Other variables of statistical significance at 0.05 level include
fire rotation and July maximum temperature. This model can be
expressed as the following form:
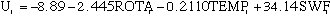
This model provided the fire occurrence probability value in each grid cell which is the importance basic of this grid automation simulation.
Grid is a raster-based geoprocessing tool that provides functions of simple and complex grid-cell analysis (Esri, 1991). The major concern of the grid based data structure is the location of the object and the neighborhood-notation processing in ArcInfo GRID module. Since the grid provides a way to create custom neighborhoods and defines the manner in which neighborhood should be processed, it is suitable for application in fire growth simulation.
The probability field of study area, which is a vector-based coverage created from the probability model of fire occurrence was converted into a grid coverage and the probability values of each grid cell was adjusted to be an integer between 0 and 100. The probability value in each grid pixel implies the influences from several factors, such as fire history, fuel, neighbor effect, and topology.
A fire is then ignited by the user at a certain location on the grid cell. Multiple ignitions can be operated in several places simultaneously. The user should specify wind direction and wind speed information and specify burning time for this fire event after the fire sources have been specified.
The x, y offset values are assigned to the surrounding cell locations from the current burning cell. Each neighboring cell is evaluated by comparing the probability value of fire occurrence in that cell and a random number generated for that cell. For each burning cell, eight random numbers between 0 and 100 are generated to determine which neighboring cells will be affected by the currently burning cell in the next step. When the generated random number is smaller than the probability of fire occurrence on a cell, this cell is the next cell ignited by the previous burning cell.
The weight of the probability of fire occurrence in eight neighboring cells is adjusted by the wind direction and wind speed. The higher probability value denotes the greater fire preference that is used to simulate the spread movement of fire across the landscape. The weights of the probability of fire occurrence have been calibrated based on partial real time burning data from the San Jacinto fires of 1996. The grid automation procedures were coded using the ArcInfo Arc Micro Language (AML).
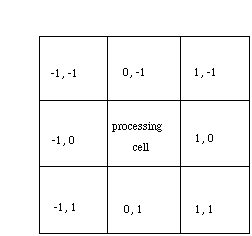
Figure 3. The x, y offset value from the current burning cell
The fuel data, percent slope, temperature, wind speed, and wind direction of simulated burned cells along with humidity data are entered into the BEHAVE system to get the rate of spread and fireline intensity data for each burned grid. The distance between two adjacent orthogonal neighbors is equal to the size of the cell; the distance between adjacent diagonal neighbors is equivalent to the size of the cell multiplied by the square root of 2. The burning time for each grid cell is equal to the distance divided by the rate of spread which is calculated from Rothermel's model. This procedure is iterated until the predefined time has been reached. The age of the burning cell is measured by the distance between the fire front and this cell. When a set distance is reached, the fire in this cell goes out. This model is calibrated based on partial real time fire propagation data of the San Jacinto fire that was recorded by a team of fire behavior personnel from an aircraft during the fire; the remaining fire propagation data is used to validate the model later on.
Another critical model employed in this project is the Rothermel's model of fire behavior. The application package of Rothermel's model for fire prediction and management, known as BEHAVE, has been widely used in the United States (Burgan and Rothermel 1984). This mathematical model was designed to predict the spread rate of fire and fireline intensity in certain fuel, weather, and topographical conditions (Rothermel 1983). The model was designed for fire in uniform continuous surface conditions and it is applying to short term fire growth prediction and requires repeated calculation. In this research, spatial data is stored in a grid structure where each grid corresponds to a uniform parcel of land. For each grid cell, the fuels, topography, and weather are allowed to vary from cell to cell but have uniform properties within the cell. The rate of fire spread and fireline intensity were calculated in the BEHAVE system. The rate of spread calculated from BEHAVE system for each grid cell was used to estimate the simulated spread distance based on the predefined time.
On June 29, record temperatures for the date were recorded in several places in Riverside County. A wildfire began in Bee Canyon Road in the afternoon and southern aspect, in a chaparral fuel type dominated by chamise. The fire burned northward, then northeast toward the Soboba Indian Reservation and Highway 243. More than 1000 acres burned on the west side of the San Jacinto Ranger District of the San Bernardino mountain.
On June 30, flames raged toward Idyllwild. Hot weather, steep terrain, and thick brush made the fire spread quickly. The prevailing wind turned hot and made the fuel more volatile. About 5000 acres of rich fuel, some untouched for several decades had been consumed by 10 p.m. (Figure 4).
On July 1, the fire went up the slopes of the mountains toward the resort communities. The temperature was still high. The winds were not so strong and the humidity was higher. The fire grew very slowly during the afternoon. The fire had consumed about 8200 acres in the San Bernardino National Forest east of Valle Vista.
On July 2, heavy clouds and higher humidity added moisture to the air and vegetation; small rains helped to dampen the fire.
On July 3, a tropical storm in Baja California brought moisture and rains. By 6 p.m. firefighters declared the fire contained. In total, 9620 acres, almost 15 square miles of grass and chaparral on the south side of the San Jacinto Mountains, were burned. Two mountain communities had been evacuated and it cost several million dollars to suppress this fire.
Compared the simulated results from the grid automation model with the fire propagation map of Bee canyon fire (Figure 4), more than 50% of actual burned cells have been identified through this model. The Rothermel's model provided the estimated spread rate ranging from 5 m/min to 37 m/min compared with observed fire spread rate ranging from 1 m/min to 87 m/min. This research provides preliminary results showing the grid automation method could be a useful way to simulate the complex fire diffusion processes over space and time.
Anderson, D.H., E.A. Catchpole, N.J. De Mestre, and T. Parkes, 1982. Modelling the spread of grass fires. J. Austral. math. Soc. (Series B). 23:451-466.
Burgan, R.E. and Rothermel, R.C. 1984. BEHAVE: Fire behaviour prediction and fuel modeling system, USDA Forest Service Research Paper, INT-167 Intermountain Forest and Range Experiment Station, Ogden, Utah.
Chou, Y.H., R.A.Minnich, L.A.Salazar, J.D.Power, and R.J. Dezzani. 1990. Spatial autocorrelation of wildfire distribution in the Idyllwild quadrangle, San Jacinto mountain, California. Photogrammetric Engineering & Remote Sensing. Vol.56(11):1507-1513.
Chou, Y.H. 1991. Map resolution and spatial autocorrelation. Geographical Analysis, 23:228-246.
Chou, Y. H. 1992. Management of wildfires with a geographical information system. International Journal of Geographical Information Systems. Vol.6(2):123-140.
Chou, Y.H., Minnich, R.A. and R.A. Chase, 1993. Mapping probability of fire occurrence in San Jacinto mountains, California, USA. Environmental management. Vol.17(1):129-140.
Chou, Y.H. 1993. Spatial autocorrelation and weighting functions in the distribution of wildland fires. International Journal of Wildland Fire. 2(4):169-176.
Environmental Systems Research Institute. 1987. ArcInfo TIN User Manual. Fundamentals of TIN, Redlands, California:Esri).
Environmental Systems Research Institute. 1991. ArcInfo User Guide. Cell- based Modeling with GRID, Redlands, California:Esri).
Fact on File-World News Digest with Index. 1993. pp824.
Fact on File-World News Digest with Index. 1994. pp20-21.
Moran, P.A.P. (1948). "The Interpretation of Statistical Maps." Journal of the Royal Statistical Society, Series B 37, 243-51.
Moran, P.A.P. (1950). "Notes on Continuous Stochastic Phenomena."Biometrika 37, 17-23.
Rothermel, Richard C. 1972. A mathematical model for predicting fire spread in wildland fuels. Research Paper INT-115. Ogden, UT:U.S. Department of Agriculture, Forest Service, Intermountain Forest and Range Experiment Station.
Rothermel, Richard C. 1983. How to predict the spread and intensity of forest and range fires. General Technical Report INT-143. Ogden, UT:U.S. Department of Agriculture, Forest Service, Intermountain Forest and Range Experiment Station.
U.S. Geological Survey, 1987. Digital Elevation Models, USGS Data User's Guide, Vol.5, p.38.
Wrigley, N., 1976. An introduction to the use of logit models in geography. Concepts and Techniques in Modern Geography, Vol. 10 (Norwich: Geo Abstracts).
Pin-Shuo Liu and Yue-Hong Chou
Department of Geosciences
University of California
Riverside, CA 92521 USA
Pin-Shuo Liu
ph:(909)787-5517
E-mail: benjamin@ucrac1.ucr.edu
Yue-Hong Chou
ph:(909)787-5513
E-mail:hong@ucrac1.ucr.edu