 (1)
(1)ABSTRACT
INTRODUCTION
A digital elevation model (DEM) is defined as "any digital representation of the continuous variation of relief over space," (Burrough, 1986, p. 39). Elevation data can be represented digitally in many ways, including a gridded model where elevation is estimated for each cell in a regular grid, a triangular irregular network, and contours. Representation of the DEM as a grid is quite common, as this format lends itself well to computer computations. This research is concerned solely with gridded DEMs. Here, the term DEM will refer to elevation represented by a regular gridded matrix.
The DEM is a computer representation of the earth's surface, and as such, provides a base data set from which topographic parameters can be digitally generated. The routing of water over a surface is closely tied to surface form (Wood, 1996), therefore hydrological features are often extracted from DEM data. From slope, flow direction can be determined; from flow direction the upslope area that contributes flow to a cell can be calculated. Upslope contributing area can be used to identify ridges and valleys. The upslope area (A) and slope (TanB) grids can be used to obtain a parameter called the topographic index (natural logarithm of the upslope contributing area per unit contour length divided by slope), expressed as ln(A/tanB). This similarity surface indicates where surface saturation is likely to occur. The DEM is therefore a valuable data source for many resource-related GIS applications.
The DEM, as its name implies, is a model of the elevation surface. However, the DEM is often not treated as a model, but is accepted as a "true" representation of the earth's surface. DEM data, like other spatial data sets are subject to error. DEM errors (discussed in detail below) are elusive and constitute uncertainty. The effect errors in a DEM are often not evaluated by DEM users. Do these errors affect results of analyses that incorporate elevation and derived topographic parameters? Maybe, maybe not. But is it safe to assume that they have no effect without a quantitative evaluation of DEM uncertainty? The purpose of this paper is to present a methodology that has been developed to provide a tool that DEM users can apply to evaluate the effect of uncertainty on elevation and the derived parameters of slope, upslope contributing area and the topographic index [ln(A/tanB)].
Currently techniques to quantify DEM uncertainty are not readily available nor are they systematically applied to DEM data used in environmental analyses. A survey of DEM users (Wechsler, 1999) evaluated perceptions of DEM uncertainty. Preliminary results indicate that, of those who responded, 50% believe they are "always or sometimes" affected by uncertainty. Twenty-two percent believe the effects of DEM uncertainty are "very important", while 57% believe these effects are either "important or somewhat important". Fifty-two percent rarely or never account for uncertainty in the DEM. In addition, users would devote only a small amount of time to evaluate uncertainty and a large percentage (59%) of DEM users reported using Esri GIS products.
The DEM User Survey results indicate that, although there is an awareness of DEM uncertainty, few DEM users apply methods to evaluate uncertainty. An uncertainty simulation method that is easily implemented within a widely used GIS environment is necessary and was developed and presented here. This methodology provides a tool by which DEM uncertainty can be addressed.
BACKGROUND
USGS DEMs
The United States Geological Survey (USGS) collects and processes elevation data and distributes it in digital formats. USGS DEM data is available in many different forms that vary in horizontal and vertical resolution, and accuracy. Highest resolution DEMs correspond to data contained in USGS 7.5 minute quadrangles at 1:24000 scale with a resolution of 10 or 30 meters. These data sets are not yet available for all areas of the nation. The focus of this research is on the USGS 7.5-minute DEM data product.
USGS 7.5-minute DEMs are two-dimensional arrays of elevations spaced evenly within the universal trans-mercator (UTM) map projection. Each elevation value represents the ground elevation found within 900 square meters (grids of 30x30 meters). Elevation values in USGS DEMs are subject to three types of errors: (1) blunders, (2) systematic errors and (3) random errors. Blunders are vertical errors associated with the data collection process. These errors exceed the maximum absolute error permitted and as such are easily identified and removed prior to release of the data. Systematic errors are the result of procedures or systems used in the DEM generation process and follow fixed patterns that can cause bias or artifacts in the final DEM product. When the cause is known or if they can be identified, systematic errors can be eliminated or reduced. Random errors result from mistakes, such as inaccurate surveying or improper recording of elevation information. Random errors result from accidental or unknown combinations of mistakes and identification of these errors is beyond the control of the DEM user. Random errors remain in the data after blunders and systematic errors are removed (USGS, 1997). It is these errors that constitute DEM uncertainty and it is these errors that are addressed by this methodology.
Measure of vertical accuracy in USGS DEMs is provided by the USGS in the form of the Root Mean Square Error (RMSE) statistic. The RMSE for USGS DEMs is calculated by comparing the DEM with 28 elevation points that reflect the "most probable" elevations at those locations (obtained from field control, aerotriangulated test points, spot elevations, or points on contours from existing source maps), not necessarily actual elevations (USGS, 1997). [In a 30-meter USGS DEM there are approximately 161,355 elevation values; the 28 verification points used for calculating the RMSE constitute 0.017% of the data set]. The RMSE is expressed as:
 (1)
(1)
where yi is an elevation from the DEM, yj is the "true" known or measured elevation of a test point and N is the number of sample points. These test points The RMSE statistic is essentially a standard deviation and is thus based on the assumption that errors in the DEM are random and normally distributed.
The RMSE, while a valuable quality-control statistic, does not provide the DEM user with an accurate assessment of how well each cell in the DEM represents the true elevation. It merely provides an assessment of how well the DEM corresponds to the data from which it was generated. However, this statistic is often the only information USGS DEM users have with which to evaluate the quality of a particular DEM. The RMSE is valuable in that it can serve as a range for use in simulation techniques. The true elevation can be expected to exist within the range provided by the RMSE.
DEM Error Constitutes Uncertainty
"In science, the word error does not carry the usual connotations of the term mistake or blunder. Error in a scientific measurement means the inevitable uncertainty that attends all measurements. As such, errors are not mistakes; you cannot eliminate them by being very careful. The best you can hope to do is ensure that errors are as small as reasonably possible and to have a reliable estimate of how large they are" (Taylor, 1997, p. 3).
Error is the departure of a measurement from its true value. Often, in geographic analysis or analysis of complex natural systems using spatial data, we do not know or do not have access to the true value. Our lack of knowledge about the reliability of a measurement in its representation of the true value is referred to as uncertainty. Uncertainty is a measure of what we do not know. Uncertainty exists in spatial databases. Unfortunately, the exact nature and location of this error cannot be precisely determined. Uncertainty refers to our lack of knowledge about this error. Sources of possible error in DEM data sets include (Burrough, 1986; Wise, 1988):
1. Data errors due to the age of data, incomplete density of observations or results of spatial sampling.
2. Measurement errors such as positional inaccuracy, data entry faults, or observer bias.
3. Processing errors such as numerical errors in the computer, interpolation errors or classification and generalization problems.
Many USGS DEMs are generated from information garnered from paper topographic maps. Many of these maps are outdated and may not incorporate topographic changes (due to development or natural occurrences). Gridded DEMs provide a discrete representation of a continuous data source. Elevation in a 30x30 grid on the ground may vary and most likely will not correspond directly with the co-located value in a DEM. In addition, elevation data in a particular grid cell is often based on sample elevation points. If the sampling scheme is inefficient, the resulting grid may be biased.
It is a practical impossibility to obtain information on the exact source and amount of error in a particular DEM. Such an undertaking would involve, for example, field measurements over an approximate 55-square-mile (35,766-acre) area. The area might be segmented into a grid of 900 square meters per grid totaling 144,801,000 grid cells within which one or more elevation readings might be measured. Even such an undertaking, if physically possible, is subject to errors. The underlying assumption of this research is that specific error within DEMs cannot be known and therefore the elevation model is replete with uncertainty.
"...error reporting for DEM data is underdeveloped, and geared more to the production process, rather than assessment of possible effects of error. Users are not provided with adequate data quality information from which to assess the effects of error with their application." (Monckton, 1994, p. 202).
Systematic errors are not easily detectable and can introduce significant bias. Many studies have investigated methods to identify systematic errors in DEMs. Brown and Bara (1994) used semivariograms and fractal dimensions to analytically confirm the presence and structure of systematic errors in DEMs and suggested filtering as a means to reduce the error. Theobald (1989) reviewed the sources of DEMs and DEM data structure to identify how bias and errors are produced in DEM generation. Polidori et al. (1991) used fractal techniques to identify interpolation artifacts in a 40-meter DEM created from a 1:25,000 scale map. The authors suggested that the fractal dimension D could be used as a DEM quality indicator by revealing directional tendency or excessive smoothing in the DEM. Carter (1992) determined that rounding the elevation values to the nearest meter significantly affected aspect (and to a lesser extent slope) calculations. Gyasi-Agyei et al. (1995) investigated the effect of vertical resolution on derived geomorphological parameters. Elevation values were rounded from the nearest centimeter and to the nearest 10 meter. The change in elevation affected individual pixel slopes, the upslope contributing area and the topographic index. However the cumulative distribution of these parameters did not show any significant change with resolution. The authors concluded that the specified vertical resolution is satisfactory for hydrologic applications (such as the extraction of channel networks) if the ratio between the average elevation drop per pixel and the vertical resolution is greater than 1 (Gyasi-Agyei et al., 1995). These finding are important in that USGS DEM products report elevations as integer values.
Errors in spatial data (such as incorrect elevation values assigned to a point) are spatially autocorrelated. For example, an error in a surveyor's benchmark measurement will affect resulting elevation values developed from that point. This spatially dependent error is unknown, thus uncertainty regarding this error is spatially dependent. This can create systematic errors in DEMs and poses a problem for non-spatial statistical methods used to define map accuracy that do not directly incorporate spatial autocorrelation of uncertainty (such as the RMSE).
Modeling Uncertainty of Spatial Data - Stochastic Simulation
The "simulation school" (Chrisman, 1989) regard a map as a distribution of possible realizations within which the true values lie. This is referred to as stochastic imaging, or the "modelling of spatial uncertainty through alternative, equiprobable, numerical representations (maps) of spatially distributed phenomena." (Journel, 1996, p. 517).
Applying this stochastic approach to error modeling requires a number of maps or realizations upon which selected statistics are performed. Uncertainty is computed by evaluating the statistics associated with the range of outputs. This process has been referred to as "finding a Gaussian distribution for maps" (Hunter and Goodchild, 1997, p. 37). From the distribution of these maps a mean and standard deviation can be obtained which relates to the true values.
"If a suitable stochastic model can be devised to model errors, then a sample of realizations of the process is generated; the analysis is performed repeatedly on each realization; and finally product uncertainty is computed by evaluating some suitable statistical summary of the range of outputs, such as a standard error" (Hunter and Goodchild, 1997, p. 36).
Stochastic simulations provide a series of random plausible maps using stochastic modeling methods from mathematical statistics. The technique does not ensure that a "real" map is generated from the process (Chrisman, 1989), but the simulation does provide a bound within which we can state the true map lies. Simulation techniques can therefore be used to represent uncertainty about the true elevation. Various methods for simulating surfaces are available (Deutsch and Journel, 1998). One of the more common simulation techniques is Monte Carlo simulation.
Various researchers have applied Monte Carlo simulation techniques to evaluate uncertainty in DEM data. Fisher (1991) applied Monte Carlo simulation techniques to evaluate the impact of DEM error on viewshed analyses. Lee et al. (1992, 1996) simulated errors in a grid DEM and determined that small errors introduced into the database significantly affected the quality of extracted hydrologic features. Liu (1994) used the Monte Carlo method to simulate errors in DEMs (as well as map unit inclusion in soil maps). Slope maps were derived from the original and disturbed DEMs and used to evaluate uncertainty in a forest-harvesting model to calculate maximum potential stumpage. Ehlschlaeger and Shortridge (1996) stochastically simulated error in a DEM to evaluate the impact of DEM uncertainty on a least-cost-path application. Hunter and Goodchild (1997) investigated the effect of simulated changes in elevation at different levels of spatial autocorrelation on slope and aspect calculations.
"Even with an understanding of the size and texture of spatial data uncertainty, it is not possible to determine what is actually 'out there' as long as there is any amount of uncertainty. All that can be achieved is the generation of representations of what may potentially be there, and the use of these potential realizations to develop a stochastic understanding of how spatial data uncertainty affects a geographic information application of any complexity" (Ehlschlaeger, 1998, p. 6).
This research provides a tool readily available to DEM users in the ArcView Spatial Analyst GIS environment to simulate uncertainty in a particular DEM and derived parameters of slope, upslope area and the topographic index.
ASSUMPTIONS
OBJECTIVES
This research applies a methodology that can be implemented within the Esri ArcView Spatial Analyst GIS environment to simulate DEM error and quantify DEM uncertainty. The method relies on characteristics of the given DEM to represent the uncertainty in elevation and its effect on derived parameters. Currently techniques to quantify DEM uncertainty are not readily available nor are they systematically applied to DEM data used in environmental analyses (Wechsler, 1999). This research provides a tool by which DEM uncertainty can be addressed. The objectives of this research are to apply the Monte Carlo DEM Uncertainty Simulation tool to a USGS DEM to quantify DEM uncertainty in the elevation data and derived parameters of slope, upslope area and topographic index.
MATERIALS AND METHODS
Representation of DEM Error as Random Fields
The methodology developed as part of the Spatial Analyst extension includes five different methods for representing DEM uncertainty in the form of random fields. A random field is simply a grid of random values, either uniformly or normally distributed, or scaled to a specified error range. For example, if the DEM being evaluated is a USGS 7.5-minute level 2 DEM with a stated RMSE of 3-meters, a uniformly distributed random field would be a grid where each value ranges somewhere between +3 and -3. A normally distributed random field would have a mean of 0 and a standard deviation of 3. Usually the DEM user is only provided with an RMSE value as an indicator of DEM accuracy. This statistic can be interpreted as the range within which a true elevation lies. If the RMSE is used as an indication of the range of error, a normally distributed random field based on this error value should be used. If the user has elevation data points deemed higher quality than a given DEM, these points can be used to calculate an RMSE, and uniformly distributed random fields within the calculated range could be applied. The uniform random field provides a more conservative estimate of error as no elevation in the DEM would be perturbed by a value that exceeds the stated range.
In nature, near entities are more related to each other than those farther away and are thus spatially autocorrelated (Ehlschlaeger, 1998). This is true for elevation data as well as for error in elevation data. For example, an elevation error arising from inaccuracy in a surveyor's tool would apply to elevations where that tool was used, say the northeast corner of a quadrangle, but would not apply to elevations gathered on a different day using a corrected tool on the southwest portion of the quadrangle. Although random errors exist, error tends to be spatially autocorrelated. Unfortunately, DEM providers do not furnish information regarding the spatial dependence or spatial relationships of error. Four different methods for representing the spatial dependence of error through random fields were developed for this research. The methods differ in the way the spatial autocorrelation of the random error is represented. Four of these methods incorporate an inherent characteristic of the DEM, the distance of spatial dependence (D).
Distance of Spatial Dependence (D) - Kernel Determination
Four of the five filters developed for the uncertainty simulation are based on an assumption that the distance of spatial dependence (D) of elevation values in a DEM can be determined from the range of the DEM's semivariogram. The distance of spatial dependence is unique to a specific DEM and is related to characteristics of the terrain. The distance of spatial dependence for an area characterized by flat plains will be further than that for highly varied glacial topography. Once determined, the distance is applied as the neighborhood or search radius of a filter.
Analysis of the semivariogram provides information about the spatial characteristics of the data set and is often used to explore spatial interdependence (Kitanidis, 1997). There are three main characteristics of the variogram the sill, range and nugget. At large values of the lag-distance (h) the plot tends to level off becoming horizontal. At this distance, the variogram has reached a sill, which is theoretically the sample variance. The distance to the sill is called the range. Within this range data points are spatially autocorrelated.
The semivariogram range can be used to indicate the distance of spatial dependence. This distance of spatial dependence is the physical distance within which elevations are related. Elevation values located within the distance of the range are spatially autocorrelated. Thus the semivariogram can provide an indication of the geographic limit of spatial autocorrelation. However, elevation data is anisotropic. The distance of spatial dependence will not be the same for different portions of a DEM. This geographic scale dependence of the semi-variogram is exemplified in Figure 1. The semivariogram for the Seager, NY quadrangle was calculated; the quadrangle was then separated into quadrants and the variogram for each quadrant calculated. The differences in the relationships between elevation data within each quadrant are evident. The appropriate D should therefore be based on the geographic extent for which information is desired.
Five Random Field Methods
Five methods were developed to represent DEM error in the form of random fields. Examples of random fields from each method are summarized in Table 1 and visual examples are provided in Figure 2.
1. Unfiltered - Worst Case Scenario
The first method of representing DEM error is through the use of an unfiltered random field (uniformly or normally distributed within an error range). This random field method assumes that errors in a DEM are completely random and not spatially autocorrelated.
It is generally recognized that DEM errors are spatially autocorrelated as opposed to random. Therefore, the uncertainty estimates generated from random unfiltered realization results are probably not realistic. Hunter and Goodchild (1997) suggest that unfiltered random fields are inappropriate for use in simulation of uncertainty because DEM errors tend to be spatially autocorrelated. It is this author's contention that a random unfiltered error field provides a "worst-case-scenario" of potential error. If the meaning of the RMSE is interpreted literally, each elevation value in the DEM has the possibility of being the given elevation, or an elevation somewhere in the range of the RMSE. This unfiltered random field method approximates this possibility.
2. Neighborhood Autocorrelation
Error is spatially autocorrelated. The neighborhood autocorrelation method increases the spatial autocorrelation of the random error field by passing a mean low pass filter in a 3x3 neighborhood over the surface. Each cell in the random field is replaced by the mean of the random values in the surrounding nine cells. This method increases the spatial autocorrelation of each random surface and decreases the standard deviation of the values. The filtered field is then added to the elevation surface to produce a perturbed realization of the true elevation.
The mean spatial dependence filter (SD) method incorporates characteristics inherent in the selected DEM and requires prior analysis of the DEM by the user to obtain the distance of spatial dependence (D). The filter passes a DxD kernel over each cell in a grid. The center cell of the kernel is replaced by the mean of the surrounding DxD cells.
4. Weighted Spatial Dependence
The weighted spatial dependence (WSD) filter further incorporates spatial autocorrelation specific to a selected DEM. The dimensions of the filter kernel are based on the determined distance of spatial dependence (D) obtained by the user in a prior evaluation. The filter passes a DxD kernel over a grid and calculates a weighted mean of all the cells within the kernel.
5. Interpolated Spatial Dependence
The interpolated spatial dependence random field method was developed to address uncertainty associated self-generated DEMs developed from surveyed points with an inverse distance weighted (IDW) interpolation. IDW uses weighted averaging techniques to fill an elevation matrix. The interpolated value of a cell is determined from values of nearby data points taking into account the distance of the cell from those input points. IDW "assumes that each input point has a local influence that diminishes with distance", (Esri, 1996). The interpolated elevation is expressed as:
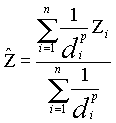 (2)
(2)
where di...d are distances from each of the n sample locations to the point being estimated, zi...zn are the sample values and p is the power of the distance. Weights are inversely proportional to the power (p) of the distance; different powers result in different estimates. As p approaches 0 weights become more similar and the inverse distance estimate approaches the average of nearby sample values. As p increases, more weight is given to the closest sample and less to those farther apart. The default power value used by ArcView GIS is "2". A neighborhood or search radius is used to define what constitutes a nearby sample. This search radius controls which samples are included in the interpolation procedure (Isaaks and Srivasta, 1989). The D value can be applied as this search radius.
The IDW random fields can be used to represent error in DEMs generated from IDW interpolated points or any other DEM. The method interpolates random error fields from a set of randomly located points with a mean of 0 and a standard deviation equivalent to the expected error (or RMSE).
The program provides two methods for obtaining these random points; the method used depends on the type of DEM being evaluated. If the DEM was interpolated from a series of surveyed points, the location of these surveyed points can be used to extract random error values from various random error fields. An IDW interpolation is then applied to these points resulting in a random error field. This approach addresses errors that might occur in the actual surveyed points. When this method is applied to non-IDW-interpolated DEMs, the random points are randomly selected from a random error field and the IDW interpolation is performed. In this case the resulting error fields provide yet another representation of random spatially autocorrelated error.
The IDW interpolation parameters allow specific characteristics of a DEM to be emulated in the resulting random field. These parameters include a (a) search radius, (b) barrier theme, and (c) power. The search radius controls the sample points selected for interpolation. The search radius can be fixed or variable. The fixed search radius has a set circular search distance with a minimum sample requirement. Interpolation is limited to samples within the fixed search radius, unless the number of samples within the radius is less than the minimum samples required. In that case the radius is expanded to include the minimum number of samples. The fixed search radius option allows the user to set the search radius based on the specified distance of spatial dependence, as determined from analysis of the DEM's semivariogram. A variable search radius has a fixed number of samples and a maximum search distance. The variable search radius finds the closest samples within the maximum search distance until the specified number of samples is achieved. If the specified number of samples does not exist within the maximum search distance, then only those samples found are used. A barrier theme can be used to limit the search radius to control selection of input points that cross features such as ridgelines. If such a theme is available, the user can select it to provide additional constraints on the interpolation. The power is the exponent of distance that controls the significance of surrounding points upon the interpolated value. With a power of 0 all point values are given equal weight. As the power increases, more weight is given to cells closer. As the power increases, more weight is given to the closest sample and less to those farther apart.
Table 1: Description of Random Field Generators
|
Random Field Method |
Description |
|
[1] Unfiltered |
Random fields based on DEM RMSE range (unfiltered). |
|
[2] Neighborhood Autocorrelation |
Mean 3x3 low-pass filter applied to [1]. |
|
[3] Mean Spatial Dependence |
Mean DxD filter applied to [1]; cells replaced with the mean of surrounding DxD cells. |
|
[4] Weighted Spatial Dependence |
Filter [1] with a weighted DxD kernel; cells farther away are assigned less weight. |
|
[5] Interpolated |
Random fields interpolated from random points with normally distributed values scaled to the error range. |
Procedure
The methodology for representing DEM uncertainty in a Monte-Carlo framework was programmed in Avenue and implemented within the ArcView Spatial Analyst environment. The methodology is based on calculation of the residuals of each parameter, or the difference between each perturbed parameter and the original unaltered parameter.
This research assumes that a given DEM is only one of an infinite number of representations of the true elevation and this original undisturbed DEM is our best or only estimate of the elevation surface. For the purposes of this research, the original DEM and the parameters resulting from it will be referred to as the true parameter values. The topographic parameters to be evaluated include (1) elevation, (2) slope [TanB], (3) upslope contributing area [A], and (4) the topographic index - ln(A/tanB).
A spatial model of the methodology is depicted in Figure 3. A DEM is selected and a random field (created by one of the five methods) is added to the DEM N times, yielding N realizations of the DEM. Four topographic parameter grids are computed from each of the N realizations (elevation, slope, upslope contributing area and the topographic index). From these N realization grids, for each parameter, twelve statistic grids are computed and provided as the results of each uncertainty simulation. Thus forty-eight result grids are produced from each simulation. Each cell for each result statistic grid represents the statistic computed from the N realizations for all data in that cell location. The result statistic grids include:
Bias
Bias measures the average deviation of the statistic and is expressed as
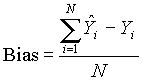 (3)
(3)
where ![]() refers to the estimator of the parameter
refers to the estimator of the parameter ![]() and N is the number of simulations (i.e. N = 125). Each cell in the bias grid represents the average amount of variation expected for that parameter at that particular location. For example, if the bias for column 1 row 1 in the elevation grid is 4, the elevation can be expected to vary, on average, ± 4.
and N is the number of simulations (i.e. N = 125). Each cell in the bias grid represents the average amount of variation expected for that parameter at that particular location. For example, if the bias for column 1 row 1 in the elevation grid is 4, the elevation can be expected to vary, on average, ± 4.
Relative Bias
Relative Bias expresses the average percent deviation of the statistic from the original value and is expressed as
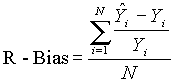 (4)
(4)
Each value in the relative bias grid can be interpreted as the percent that location is expected to deviate under the simulated uncertainty conditions.
Average Relative Absolute Difference (ARAD)
The average relative absolute difference (ARAD) between a perturbed parameter and the true value measures the average percent absolute deviation of the perturbed parameter (Li, 1988, Desmet, 1998). This statistic is similar to the relative bias however, all values are reported as positive and hence are intuitively more straightforward. ARAD is expressed as:
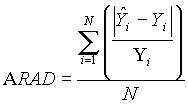 (5)
(5)
Root Mean Square Error (RMSE)
The RMSE is a commonly employed measure of estimator performance. The RMSE is used by the USGS to indicate vertical accuracy of an entire grid. Here, the RMSE grid represents the expected accuracy of each cell under the simulated uncertainty conditions. The RMSE is expressed as:
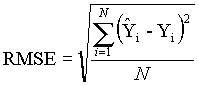 (6)
(6)
Relative Root Mean Square Error (R-RMSE)
The relative root mean square error (R-RMSE) standardizes the RMSE computed per cell to the true value observed in that cell location. The resulting R-RMSE value is expressed as a percent and represents the standard variation of the estimator. The R-RMSE assigns equal weight to any overestimation or underestimation of the statistic. R-RMSE is expressed as (Kroll and Stedinger, 1996):
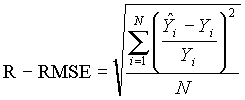 (7)
(7)
Log Root Mean Square Error (L-RMSE)
The Log Root Mean Square Error (L-RMSE) statistic assigns more weight to underestimation than overestimation and is expressed as (Kroll and Stedinger, 1996):
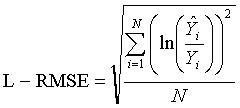 (8)
(8)
The perturbed value is standardized to the true value and the natural logarithm is computed. Placing the RMSE into log space further standardizes the distribution.
Average and Standard Deviation of N Simulations
The average and standard deviation of N simulations grids are surfaces where each cell represents either the average or standard deviation of all the perturbed values at that location. These statistics are expressed in equations 9 and 10 where ![]() represents the mean of the N perturbed parameters.
represents the mean of the N perturbed parameters.
Average of N Simulations = 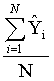 (9)
(9)
Standard Deviation of N Simulations = 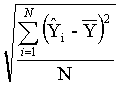 (10)
(10)
Average and Standard Deviation of N Simulations
The average and standard deviation of N residual grids are surfaces where each cell represents either the average or standard deviation of all the residuals between the perturbed and true values at a particular location. These statistics are expressed in equations 11 and 12.
Average of N Residuals = 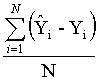 (11)
(11)
Standard Deviation of N Residuals = 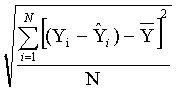 (12)
(12)
Maximum and Minimum of N Residuals
The maximum and minimum result grids are surfaces where each cell represents either the maximum or the minimum residual for a particular parameter.
DISCUSSION: APPLICATION OF SIMULATION RESULTS
The DEM user now has many ways to quantify DEM uncertainty. This research does not attempt to provide the ultimate answer as to whether DEM uncertainty is an issue. The answer to this question depends on many factors including topography, DEM quality, DEM production method and most importantly, the ultimate use of the DEM product.
The DEM Uncertainty Simulation Tool can be applied to both research questions and practical applications. The following sections describe ways in which this tool can be applied.
Research Applications of the Methodology
Case 1: Effect of Uncertainty on Topographic Parameters
This section describes how the Uncertainty Simulation Extension can be applied to evaluate the effect of uncertainty in elevation and topographic parameters for one particular DEM. The methodology was applied to a DEM corresponding to the USGS level-2 7.5-minute quadrangle for Seager, NY (Figure 4). The quadrangle falls mainly in Ulster County and partly in Delaware County, New York. The headwaters of the Beaver Kill River are located in the southwest portion of the quadrangle. The quadrangle lies within the Catskill Mountain area of the Appalachian Plateau province. The topography within this area is characterized by ridges and valleys relatively evenly distributed throughout the quadrangle. Elevations range from approximately 467 to 1181 meters and are normally distributed (skew of -0.021).
The appropriate number of simulations for this DEM was obtained using a tool provided as part of the extension. This "Determine number of N" tool takes a DEM and simulates error N times. For each N simulation a standard deviation grid is produced, and the standard deviation value pertaining to that standard deviation grid is recorded. The procedure is repeated for different N values. The appropriate number of simulations to apply can be approximated by plotting the standard deviation value for these standard deviation grids. The method is based on the theory of diminishing returns, where an increase in the number of simulations does not lead to a substantial decrease in the variability of the perturbed grids. This "appropriate" number of simulations is based on the N at which the cumulative difference in the overall standard deviation of the standard deviation grid decreases to approximately 10% as the corresponding N of 125 provides a manageable number of simulations (Figure 5). The unfiltered random field method was applied with an N of 125 random fields scaled to a normally distributed range of ± 5 meters (corresponding to the DEM's stated RMSE).
The uncertainty simulation extension program provides DEM users with a plethora of statistical grids with which to quantify DEM uncertainty. Although 48 statistical grids are generated (12 for each of the 4 parameters) for the purposes of this paper, only the RMSE grids will be used to represent the effect of DEM uncertainty on elevation and derived parameters.
Results from this simulation experiment indicate that uncertainty in the DEM is manifested in higher elevations and steeper slopes on the slope and elevation maps. However, the lower valley areas are much more sensitive to error in the data in the upslope contributing area map (errors in these areas incorporate all the upslope area error) and this is in turn reflected in the topographic index map [ln(A/tanB]. These results are illustrated by a layout of the RMSE maps for each of the topographic parameters (Figure 6). The grids can be exported to points and exported for numerous analyses in statistical and graphing packages. Some packages have a limitation to the number of values that can be analyzed. Because of this limitation the extension allows a user to randomly select points (i.e. 10,000 of the possible 140,000 in a 7.5-minute 30-m DEM) from the result grids and extract those points to a file for import into standard graphing packages (such as Microsoft Excel).
Figure 7 depicts the relationships between elevation and the RMSE of elevation as well as elevation and the RMSE of the topographic index. (All points in the DEM were used in these graphic analyses using StatGraphics version 3.3).
A simple linear regression was conducted to describe the relationships between Elevation and RMSE Elevation and between Elevation and RMSE of the Topographic index [ln(A/tanB)].
For the Elevation versus RMSE Elevation, the equation of the fitted model is: RMSE Elevation = 4.47393 + 0.000524928*Elevation. Since the P-value in the ANOVA table is less than 0.01, there is a statistically significant relationship between RMSE Elevation and Elevation at the 99% confidence level. The R-Squared statistic indicates that the model as fitted explains 3.42551% of the variability in RMSE Elevation. The correlation coefficient equals 0.185081, indicating a relatively weak relationship between the variables. The standard error of the estimate shows the standard deviation of the residuals to be 0.380086. This value can be used to construct prediction limits for new observations.
The equation of the fitted model for the Elevation versus RMSE Topographic Index [ln(A/tanB)] is: RMSE Topographic Index = 3.90124 - 0.00256589*Elevation. The P-value in the ANOVA table is less than 0.01 indicating a statistically significant relationship between RMSE Topographic Index and Elevation at the 99% confidence level. The R-Squared statistic indicates that the model as fitted explains 15.1252% of the variability in RMSE Topographic Index. The correlation coefficient equals -0.388911, indicating a relatively weak relationship between the variables. The standard error of the estimate shows the standard deviation of the residuals to be 0.82747. This value can be used to construct prediction limits for new observations.
Case 2: Effect of DEM Scale on Uncertainty
The extension tool is currently being applied to evaluate how uncertainty is manifested at different DEM scales as expressed by DEM grid cell resolution. There are 4 DEMs available for the Seager, NY 7.5-minute quadrangle: two 30-m resolution DEMs generated from different interpolation methods (USGS level-1 and level-2), one 10-m DEM and one 70-m DEM. The tool is being applied to all four DEMs and uncertainty results will be evaluated. The effect of DEM scale on uncertainty estimates will be investigated.
Case 3: Effect of Uncertainty in Different Topographic Regions
DEM uncertainty in elevation and the selected topographic parameters is being evaluated for differing types of topography (i.e. flat versus steep). The Redlands, CA quadrangle (home of Esri) provides an excellent example of different terrain. The southwest portion of the quadrangle is quite steep while the northwest portion is relatively flat. Uncertainty simulations for the entire quadrangle as well as for the flat and step portions of the area are being conducted to investigate the effect of topography on resulting uncertainty estimates.
Practical Applications of the Methodology
Case 1: Floodplain Management
Elevation data can be applied to set demarcations for areas susceptible to floods. Error in the DEM may have an impact on resulting boundaries. Policy makers and insurers should to be aware of the impact potential DEM error may have. An initial investigation was applied to data from the Seager, NY quadrangle. The 100-meter contour lines were computed for the original DEM data. An uncertainty simulation was performed. Normally distributed random fields (N=125) in the range of 5-meters were generated and added to the elevation data. The grid representing the maximum and minimum of the residuals was both added and subtracted from the original DEM and contour lines computed from each DEM rendition. An extracted portion of this map is presented in Figure 8. The determination as to whether the subtle differences in these contours matters will be based on the ultimate application of the DEM analysis.
Case 2: Nonpoint Source Pollution
Distributed parameter models require data such as slope, aspect upslope area and flow direction. Such models distribute watershed information through a grid representation. Therefore DEMs are often used to generate the input model parameter data. The effect of uncertainty in the DEM and derived data on model output can be determined using the result grid data from the uncertainty simulation analyses to parameterize the model. Rather than running a model 125 times with perturbed elevation, and another 125 times with perturbed slope parameters, (etc.) the model can be run 3 times. One run would parameterize the model with parameters obtained from an unaltered DEM. The model could then be run with a DEM with the maximum residual grid added to it, and a third time with the minimum residual grid added to it. These three models could provide a range of output potential model output while reducing the need for simulating the actual model run 125 times. Perhaps uncertainty doesn't affect the model output, but perhaps it does. The decision-maker now has a range of output that can provide a more precise representation of potential nonpoint source pollutant export from a particular watershed.
Case 3: 3-D Visualization of Uncertainty
The power of 3-D visualization can be used to portray the effects of DEM uncertainty. This type of visualization can be employed to animate potential realizations. Critical areas in a DEM (such as watershed outlets or steep slopes) can be investigated up-close through fly-by scenarios. The quantitative statistical result grids can be combined with this visualization tool to enhance our understanding of the potential effects of DEM error.
CONCLUSIONS
Errors in DEMs constitute uncertainty that can be quantified within a Monte Carlo Simulation framework. The determination as to whether this uncertainty will impact a particular application rooted in DEM data should not be made without quantitative evaluation of DEM uncertainty. This paper introduced a new suite of methods for evaluating uncertainty in DEMs and selected derived topographic parameters. Five different methods for representing DEM uncertainty were developed and implemented within an ArcView Spatial Analyst extension.
This paper presents a methodology to quantify DEM uncertainty. The purpose of this methodology is to take a step back; to provide DEM users with a suite of methods by which DEM users can evaluate the effect of uncertainty in DEMs and selected derived topographic parameters. Until now, DEM users would often apply the DEM as a truth surface rather than as a model (as its name implies). DEM uncertainty may not matter, but it is not safe to make this judgement without a thorough evaluation. The determination as to whether DEM uncertainty will impact a particular application rooted in DEM data cannot be made without quantitative evaluation of DEM uncertainty.
It is the responsibility of the DEM user to determine whether uncertainty in the DEM will affect results from specific analyses that utilize data derived from a particular DEM. This research provides the DEM user with a suite of methods to assist in this assessment. Use of this tool could result in more responsible use of DEM and derived data.
REFERENCES
Brown, D. and Bara, T. (1994), Recognition and Reduction of Systematic Error in Elevation and Derivative Surfaces from 7.5-Minute DEMs, Photogrammertic Engineering and Remote Sensing, Vol. 60, No. 2, p. 189-194.
Burrough, P. and McDonnell, R. (1998) Principles of Geographic Information Systems, Oxford University Press, New York, NY, 333 pp.
Carter, J., (1992), The Effect of Data Precision On The Calculation Of Slope And Aspect Using Gridded DEMs, Cartographica, Vol. 29, No. 1, p. 22-34.
Chrisman, N., (1989), Error in Categorical Maps: Testing versus Simulation, Auto-Carto 9: Proceedings of the 9th International Symposium on Computer-Assisted Cartography, ASPRS/ACSM, p. 521-529.
Deutsch, C. and Journel, A., (1998), GSLIB Geostatistical Software Library and User's Guide, Oxford University Press, New York, NY, 369 pp.
Ehlschlaeger, C., R., (1998), The Stochastic Simulation Approach: Tools for Representing Spatial Application Uncertainty, Ph.D. Dissertation, University of California, Santa Barbara, 1998.
Ehlschlaeger, C., and Shortridge, A., (1996) Modeling Elevation Uncertainty in Geographical Analyses, , Proceedings of the International Symposium on Spatial Data Handling, Delft, Netherlands, 9B.15-9B.25.
Esri, 1996. ArcView Spatial Analyst, Environmental Systems Research Institute, Inc., Redlands, 147 pp.
Evans, I., (1998), What Do terrain Statistics Really Mean?, In: Landform Monitoring, Modelling and Analysis, Edited by S. N. Lane, K. S. Richards and J. H. Chandler, John Wiley and Sons, 300 pp.
Gyasi-Agyei, Y., Willgoose, G., and De Troch, F., (1995), Effects of Vertical Resolution and Map Scale of Digital Elevation Models on Geomorphological Parameters Used In Hydrology, Hydrological Processes, Vol. 9, p. 363-382.
Hunter, G. and Goodchild, M., (1997), Modeling the Uncertainty of Slope and Aspect Estimates Derived From Spatial Databases, Geographical Analysis, Vol. 29, No. 1, p. 35-49.
Isaaks, E. and Srivasta, R., (1989), An Introduction to Applied Geostatistics, Oxford University Press, New York, NY, 561 pp.
Journel, A., (1996), Modelling uncertainty and spatial dependence: stochastic imaging, International Journal of Geographical Information Systems, Vol. 10, No. 5, p. 517-522.
Kroll, C. and Stedinger, J., (1996), Estimation of moments and quantiles using censored data, Water Resources Research, Vol. 32, No. 4, p. 1005-1012.
Lee, J., (1996), Digital Elevation Models: Issues of Data Accuracy and Applications, Proceedings of the Esri User Conference, 1996.
Lee, J., Snyder, P., Fisher, P., (1992), Modeling the Effect of Data Errors on Feature Extraction From Digital Elevation Models, Photogrammertic Engineering and Remote Sensing, Vol. 58, No. 10, p. 1461-1467.
Liu, R., (1994), The Effects of Spatial Data Errors on the Grid-Based Forest management Decisions, Ph.D. Dissertation, State University Of New York College Of Environmental Science and Forestry, Syracuse, NY, 209 pp.
Monckton, C., (1994), Chapter 14: An Investigation into the spatial structure of error in digital elevation data, In: Innovations in GIS Volume 1 Edited by M. Worboys, Taylor and Francis, Bristol, PA, 267 pages.
Polidori, L., Chorowicz, J., and Guillande, R., (1991), Description of Terrain as a Fractal Surface and Application to Digital Elevation Model Quality Assessment, Photogrammertic Engineering and Remote Sensing, Vol. 57, No. 10, p. 1329-1332.
StatGraphics Plus Version 3.3 Software, Manugistics, Inc., 2115 East Jefferson St., Rockville, MD 20852.
Taylor, J., (1997), An Introduction to Error Analysis: The Study of Uncertainties In Physical Measurements, University Science Books, Sausalito, CA, 327 pp.
Theobald, D., (1992), Chapter 9: Accuracy and Bias Issues in Surface Representation, In: The Accuracy of Spatial Databases, Edited by Michael F. Goodchild and Sucharita Gopal, Taylor and Francis, Bristol, PA, pp. 99-106.
United States Geological Survey (USGS), (1997), Standards For Digital Elevation Models, Department of the Interior, Washington, DC.
Wechsler, S., (1999), Results of the DEM User Survey, http://web.syr.edu/~srperlit/survey.html
Wood, J., (1996), The Geomorphological Characterization of Digital Elevation Models, Ph.D. Dissertation, Department of Geography, University of Leicester, Leicester, UK, 1996.
Wise, S., (1998), The Effect of GIS Interpolation Errors on the Use of Digital Elevation Models in Geomorphology, In: Landform Monitoring, Modelling and Analysis, Edited by S. N. Lane, K. S. Richards and J. H. Chandler, John Wiley and Sons, 300 pp.
Suzanne P. Wechsler, MS, Ph.D. Candidate,BR
State University of New York
College of Environmental Science and Forestry
1 Forestry Drive
Syracuse, NY 13210