Decisions in spatial modeling processes are often based on uncertain knowledge. This is - among others - due to inaccurate information, lack of proper data or even ignorance. One way to cope with such uncertainties is using 'belief functions'. These originate in the probability theory. Well-known key items are BAYES Theorem and DEMPSTER-SHAFER Theory. Alternative outcomes of a model form a hierarchical structure of hypotheses and their combinations. Information required and available for the modeling process is 'pooled' and aggregated to output a new probability value.The author shows a practical implementation of this process in Arcview.
"Belief modeling"? Not a common technique among spatial analysts so far, most of you might even never heard about it. Belief modeling is not a single unique method, but consists of a whole family of related ways to cope with uncertainties, incomplete knowledge and other inaccurate informations. Most of the research is done in the artificial intelligence fields. This paper focuses on the implementation of one of these techniques - the DEMPSTER-SHAFER algorithm. It does not stress mathematical and statistical issues in detail.
Originally developed by probabilistic statisticians throughout the late 1960 - 70 these method (as well as the related ones) gained more and more interest during the past ten to fifteen years. Arthur Dempster laid the foundation with his article 1967 (DEMPSTER 1967) and his student Glenn Shafer formulated a detailed explanation in 1976 (SHAFER 1976). His work remains the central basis for all studies in the DEMPSTER-SHAFER theory.
As noted above the method is used to cope with uncertain and incomplete knowledge (data, informations, ...). If we apply this to spatially related problems, it can be easily seen that many (or even most) of spatial analysis and spatial modeling questions consist of various moments of uncertainty: inaccurate measurements, incomplete knowledge about natural processes, anecdotic information, data from different scales, expert knowledge and many more.
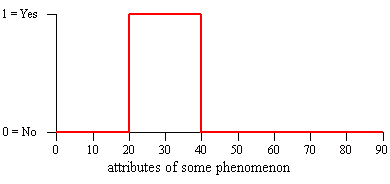
What if we are requested to aggregate all these pieces of information to model or simulate a process, a probability of occurence, a suitabilty for some landuse, etc.? The data will originate from probably very different sources, some of them might be accurate others are very soft and fuzzy. Standard case during the vectormodel-reigned GIS years could be to reclassify all the single informations by hard and crisp decisions (see figure below) and feed it into some 'overlaying' process resulting in a mess of tiny polygon snippets. Working on the basis of probabilistic informations is thus better accomplished by using rasterized data:

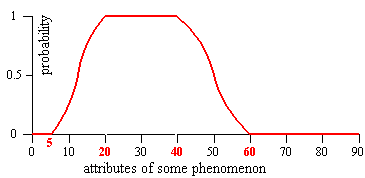
The belief modeling process involves reclassification too, but in a much smoother way: all of our information input into the analysis process is being converted to degrees or weights of belief into the support for one or the other stated outputs of the analysis (e. g., suitable/not-suitable, habitat/no-habitat, ...). In fact the weights of belief are expressed as probability values ranging from 0 to 1:
What follows now is the description of a fictitious case study to demonstrate the principles of how to implement a very simple belief model in Arcview. The chosen parameters might not be realistic from the biologists point of view, the data are meant to feed the analysis process primarily.
Let us assume to be ornithologists interested in the question "where do all the birds breed?" - we observe a certain bird species and would like to model potential habitats or nesting locations. To accomplish this task we are pooling together all the available knowledge about the habitat preferences of this species and all the various informations, that could help us determining the potential locations.
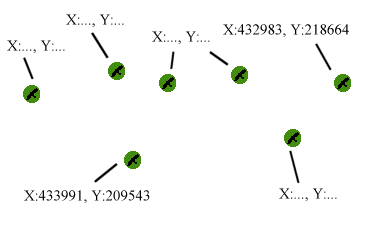
One first-class information are the already existing observations (known locations) made by us and other professional ornithologists:
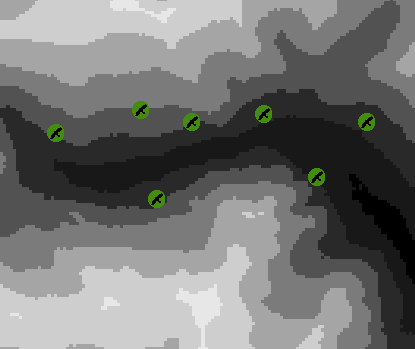
From many observations it seems to be agreeable among experts that our bird species never breeds above altitudes of 2400 m:
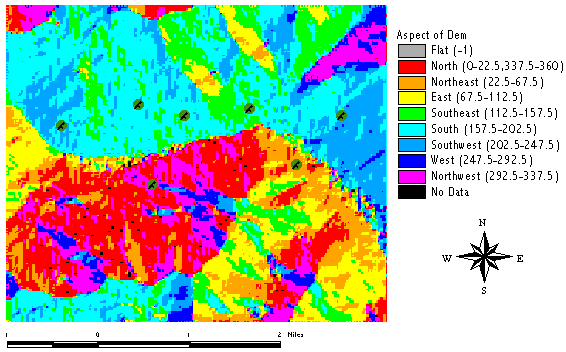
And most of the birds observed so far seemed to prefer more or less south-faced slopes:
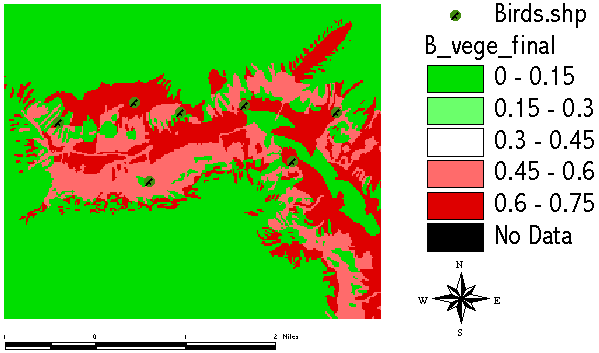
Another piece of information is our knowledge about the what the birds feed on - specific insects which generally can be found in certain plant communities. We can derive this information from a vegetation map:
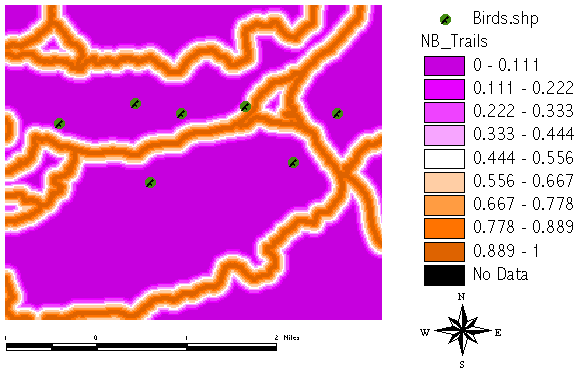
The birds are shy animals and avoid building their nests too close to the existing and frequently used trails:
We also know of a closley related bird species which competes with our species for food. But we don't have exact habitat observations about that other species. All we know for certain is that they prefer to breed nearby water streams:
Next step is to build the frame of discernment (or universe of discourse or state space, SMETS 1994; EASTMAN 1997 uses the term decision frame). This comprises all the possible alternatives (hypothesis) and all of their combinations:
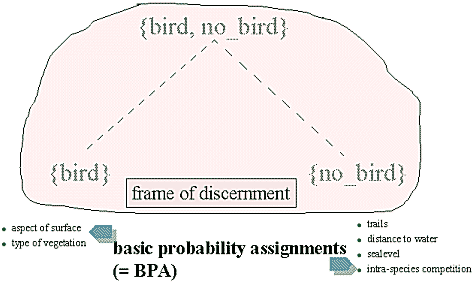
Our various pieces of evidence are assigned to support one or the other possible outcome. Later we will combine them to so-called basic probability assignments (BPAs).
Before we are able to start the aggregation process, all of our pooled evidences must be converted to represent our strength of belief. The aspect data are simply reclassified so that areas with aspects rangeing from 112 - 248° support with a degree of 0.75, other areas with 0.25 and flat areas with 0.5:
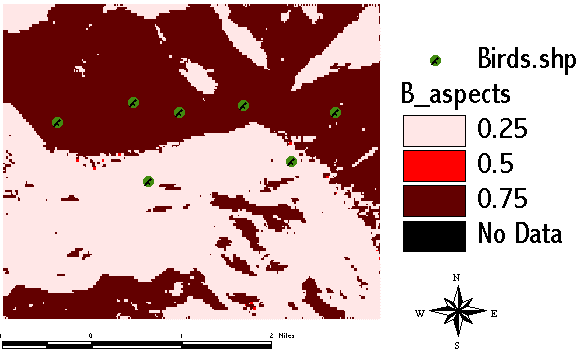
The computation in the Spatial Analyst Map Calculator (the author used the prefix B_ for all data supporting the outcome [bird]):
B_Ascpect ((([Aspect of Dem] > 112) and ([Aspect of Dem] < 248)) * 0.75) + ((([Aspect of Dem] >= 248) and ([Aspect of Dem] <= 360)) * 0.25) + ((([Aspect of Dem] >= 0) and ([Aspect of Dem] <= 112)) * 0.25) + (([Aspect of Dem] = -1)*0.5)
From the vegetation map we derive those areas with plant communities hosting our birds prefered food:
We proceed with building up those data supporting the hypothesis [no_bird], starting with the distance to existing trails. With increasing distance to trails probability for [no_bird] decreases. A linear fuzzy type function has been used in this case:
Computation as follows:
(( [Distance to Trails.shp] = 0)*1.0) + ((([Distance to Trails.shp] > 0) and ([Distance to Trails.shp] < 300))*(([Distance to Trails.shp] - 300)/(0.0 - 300)))
The information about the other related species which breeds close to water streams:
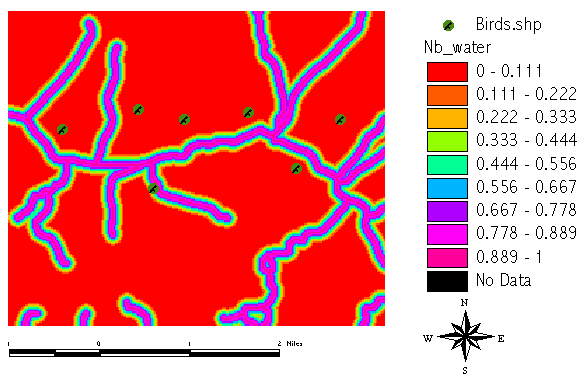
With increasing distance the support for [no_bird] decreases. The decrease follows a linear fuzzy type function between 0 and 200 m distance:
(( [Distance to Water.shp] = 0)*1.0) + ((([Distance to Water.shp] > 0) and ([Distance to Water.shp] < 200))*(([Distance to Water.shp] - 200)/(0.0 - 200)))
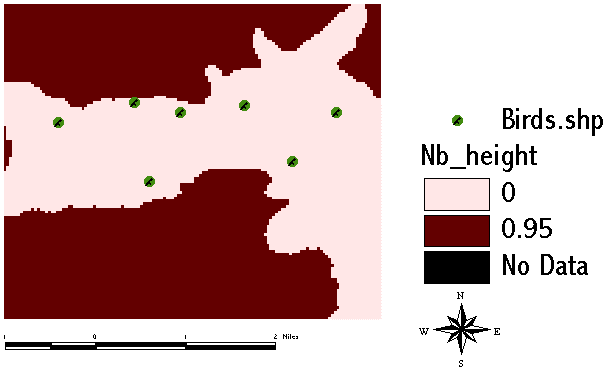
Altitudes above 2400 m are assigned a value of 0.95 to express strong support for [no_bird] in these areas:
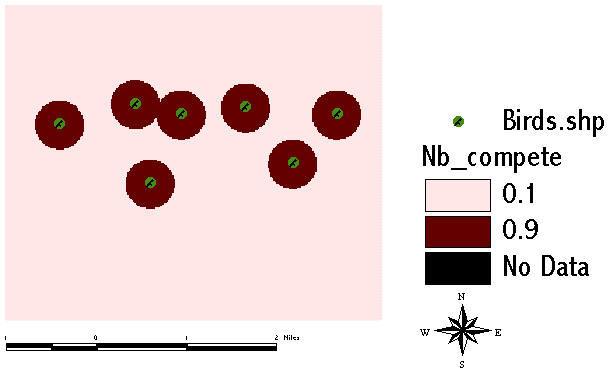
Last but not least the intra-species competition, which means, that our bird does not allow other birds of same species to breed within some distance around its own nest (in this case a radial distance of 500 m has been assumed):
The DEMPSTER-SHAFER rule for aggregation of our pooled evidences:
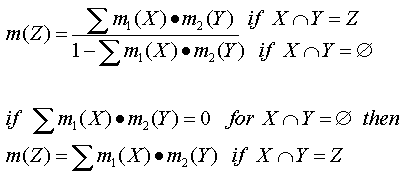
m(X), m(Y) denote the summed BPAs for the possible alternatives (m originates from the term mass assignment). The computation is no simple summation but the so-called orthogonal sum to honor the rule, that the sum of all BPAs must equal 1 anytime. What the formula does is simply to sum all the available pieces of information successively.
We start with computing the BPA[bird]. The alternative [bird] is supported by two evidences - food information (the areas of the prefered insects derived from the vegetation map) and the aspect (south-faced slopes):

([B_vege_final] * [B_aspects] )+ ((1.AsGrid - [B_vege_final])* [B_aspects])+ ((1.AsGrid - [B_aspects]) * [B_vege_final])
If we had no further informations, this result would represent the final BELIEF[bird]:
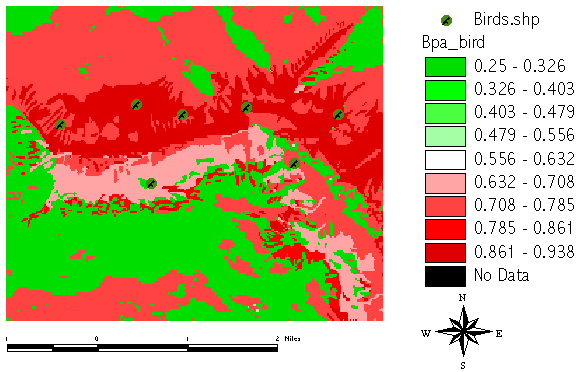
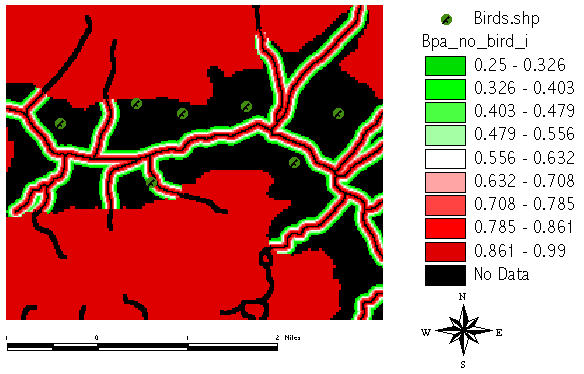
But we do have more knowledge which helps us to specify the habitat in more detail. We proceed with aggregating the facts supporting [no_bird] - the first part combines our data about the competing bird species (which breeds close to water streams) with the altitude knowledge:

Again the Map Calculator input:
([Nb_water] * [Nb_height]) + ([Nb_height] * (1.AsGrid-[Nb_water])) + ([Nb_water] * (1.AsGrid - [Nb_height]))
and the intermediate grid result:
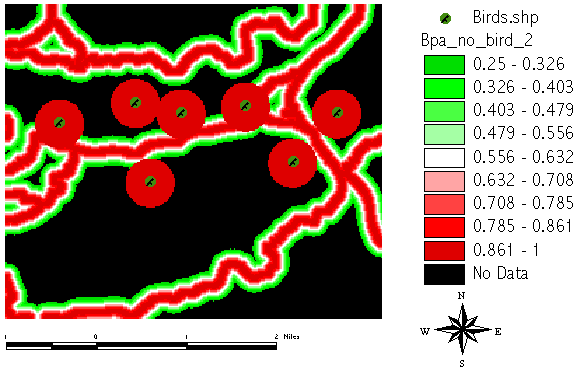
The second part in computing the BPA[no_bird] includes trails and intra-species competition:

The input for the Map Calculator:
([Nb_compete] * [NB_Trails]) + ([Nb_compete] * (1.AsGrid - [NB_Trails])) + ([NB_Trails] * (1.AsGrid - [Nb_compete]))
and the second intermediate grid:
In a third step we can finally aggregate the two previous BPA parts into the BPA[no_bird] result:
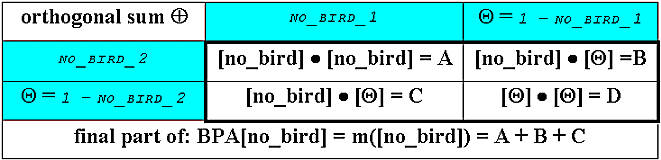
Computation shown as text again:
([Bpa_no_bird_i] * [Bpa_no_bird_2]) + ([Bpa_no_bird_2] * (1.AsGrid - [Bpa_no_bird_i])) + ([Bpa_no_bird_i] * (1.AsGrid - [Bpa_no_bird_2]))
Compare the BPA[no_bird] grid as opposed to the BPA[bird] created before:
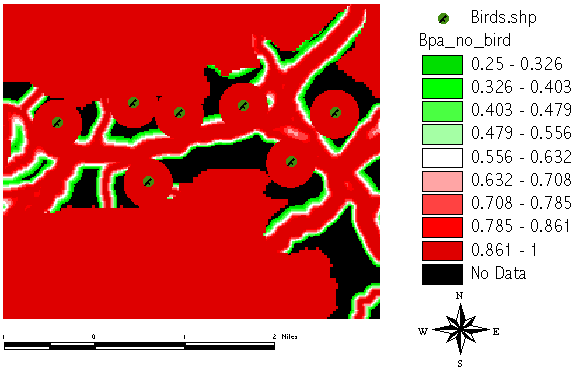
In the last step we are now able to combine all the pieces to compute the final BELIEF[bird]. This special way of computing is known as "normalization" and necessary to cope with conflicting evidences:

Map Calculator input is simple:
([Bpa_bird] * (1.AsGrid-[Bpa_no_bird]))/(1.AsGrid - ([Bpa_bird] * [Bpa_no_bird]))
And the following grid result shows the BELIEF[bird] which represents all our strong facts in the hypothesis [bird]:
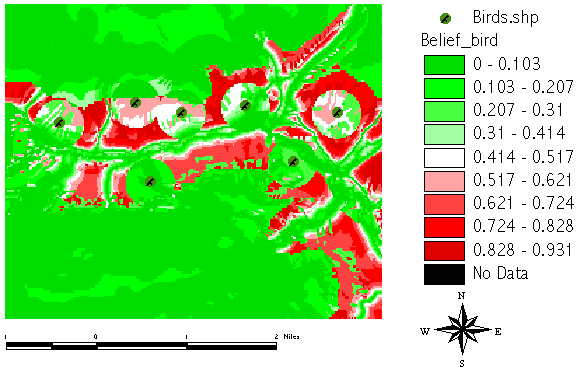
But the BELIEF result shows what we perhaps already expected, as it aggregated all our facts. What is even more interesting is the so-called PLAUSIBILITY. It denotes the degree, to which we cannot reject our hypothesis ([bird] in this case), but where we do not have strong evidence! PLAUSIBILITY[bird] is computed by 1 - BELIEF[no_bird], so it represents our ignorance, our lack of knowledge to support [no_bird]:
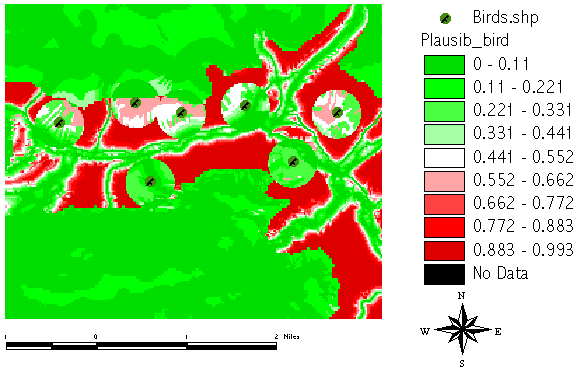
The difference between BELIEF and PLAUSIBILITY is the BELIEF INTERVALL. In areas with high BELIEF INTERVALL we do not have strong evidence but it seems to be very plausible from all our soft knowledge. It's those areas where further investigation will gain most additional and valuable knowledge:
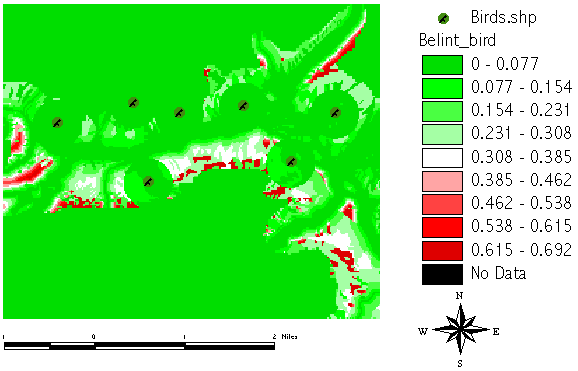
The DEMPSTER-SHAFER method is no black-box type of computation, which means, that it is not apropriate to be used just by simply pressing buttons. It allows for many configurations, as you might have noticed during the chapter about the conversion of our knowledge into degrees of belief. But the method can handle virtually all kind of data types, it is a means to quantify subjective judgements. It may be helpful to make expert decisions transparent or iterable. It should also be noted that the computational complexity very rapidly increases with larger sets of alternatives.
Instead of a fictitious example such as the current one, a real-world problem has to be tested to check for sensibility.
A more usable implementation requires Avenue programming and the design of a more-userfriendly input interface. Work on this is currently in progress and will be demonstrated on occasion.
DEMPSTER, A. P. (1967): Upper and Lower Probabilities induced by a Multivalued mapping. - Annales of Mathematical Statistics, 38: 325-339
EASTMAN, R. J., (1997): Idrisi for Windows User�s Guide, Version 2.0. � Worcester: Idrisi Project, Clark University
SHAFER, G. (1976): A mathematical theory of evidence. - Princeton: Princeton Univ. Press
SMETS, P., 1994: What is Dempster-Shafer�s model? � in: R. R. YAGER,J. KACPRZYK & M. FEDRIZZI (Eds.), Advances in the Dempster-Shafer Theory of Evidence. � New York: Wiley, 5-34
Author:
Eric J. LORUP
Dept. of Geography and Geoinformation Salzburg University
A-5020 Salzburg, Hellbrunnerstr. 34, Austria/Europe
Tel. +43(0)662 8044 5235 Fax +43(0)662 8044 525
Email: eric.lorup@sbg.ac.at
WWW: http://www.sbg.ac.at/geo/people/elorup.htm