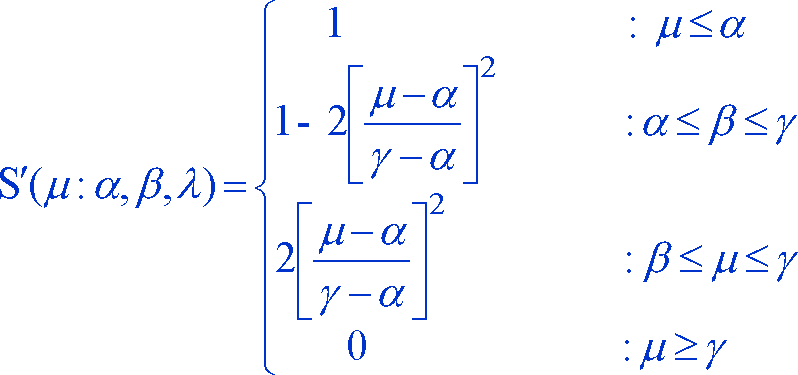
A GIS for Decision Support would normally involve integration of images, spatial layers, attribute information and an inference based on these. The different spatial layers may combine in a non-linear way and moreover the information obtained from each layer may be inaccurate or uncertain to various degrees. These uncertainties should be taken into consideration when the various items of information are combined without which the decision-making process might lead to inaccurate decisions. Hence, we propose to use Fuzzy Inferencing to handle uncertainties such as sharp class boundaries, measurement uncertainties, linguistic knowledge, and inherent uncertainty due to mixture of classes.
1. IntroductionA Decision Support System means a system that aids in making decisions and involves goals and constraints that need to be met. This could also be termed a Multi-Criteria Analysis system, i.e., a system that involves satisfying a set of criteria or constraints. This system could be called a Fuzzy Decision support System if the criteria involved are fuzzy in nature. For example, Mrs X, could be looking for a house to buy and she might have various constraints such as `a house within a mile from a highway exit, within 15 minutes walking distance from a School, that which costs around $300,000, a house that is not within a flood zone, a house that is on gentle slope etc. A multi-criteria analysis involves selecting features that satisfy a certain set of criteria.
There is a lot of work done on Error analysis in GIS and most of these deal with errors in the data which occur mainly due to the source of the data. While there has been a lot of emphasis on these types of error, there is another class of errors that find their way into analysis and these are mostly neglected. In fact, we believe that even if we have highly accurate data, we cannot achieve accurate results or make accurate decisions unless the analysis is done accurately. Analysis techniques in conventional GIS software do not consider for logical inaccuracies i.e., inaccuracies that arise due to human thinking, perception, vague concepts, unreliable measurements, lexical imprecision, etc., and assume that all variables in a problem are well-defined. GIS is mostly used to handle real-world problems and in reality, no real world decision-making problem can have precise variables. In fact, much of human reasoning is approximate rather than precise in nature. A simple example would be in proximity analysis, wherein we would like to extract certain spatial features that exist within a particular distance, say for example, 1 mile. A conventional GIS software when instructed to do this proximity search, will extract features that are exactly within a mile. But, if there is a feature of interest even as close to the boundary as 1.0000001 mile, these software cannot locate it. This is a serious logical error that is not handled in conventional methods of GIS analysis. With the ever increasing demand for accurate results, there is a demand for making the analysis intelligent, rather than it being able to perform strictly just what was insructed. Hence, what is needed is a Fuzzy proximity analysis that can handle the situation intelligently. Similarly, there are also other logical and numerical uncertainties that have to be considered for an efficient GIS analysis. Moreover, all the criteria involved in the analysis may not equally influence a decision and hence the relative importances of the criteria should also be considered. Fuzzy Reasoning provides an easy way of incorporating the relative importances. This paper explains some of the inaccuarcies that are seen in a multicriteria analysis and the methods to handle them using Fuzzy Logic.
2. MethodologyAny multi-Criteria analysis using a GIS would involve integration of various spatial layers and retrieving features that satisfy a certain set of criteria. Hence, to use a Fuzzy Analysis, two major steps are involved:
1. identifying the criteria that are fuzzy and defining their individual membership functions and
2. aggregating the different fuzzy criteria to retrieve the features that satisfy the criteria.
2.1 Membership functions of fuzzy criteria:
Membership functions are functions that reflect the degree of closeness of a feature to the criterion to be satisfied. Different types of fuzzy criteria need different functions to evaluate the memberships. We deal with three types of fuzzy criteria here.2.1.1 First, we consider the case when fuzziness is in the classification of variables due to the usage of sharp class boundaries. This is the kind of fuzziness that exist in proximity analysis, where we would not want to reject a feature just because it does not satisfy a criterion to a negligible degree. Considering the previous example of looking for an ideal house to buy, if all criteria were satisfied by a house except for one proximity criterion, say, the house is at 1.05 miles from a highway exit, then a conventional buffering would reject this house, but it is quite obvious that we would want to compromise on this one. This problem can be resolved by using a Fuzzy proximity analysis. A slightly modified version of Zadeh's S function can be used for Fuzzy proximity. The parameters of this Fuzzy Membership function can be adjusted to meet the needs of a specific application.
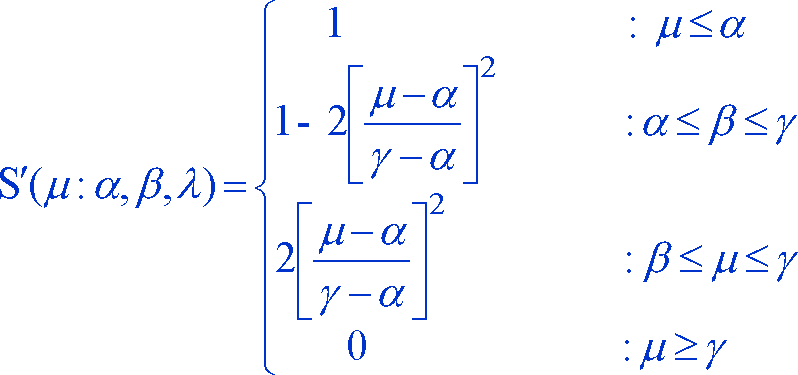
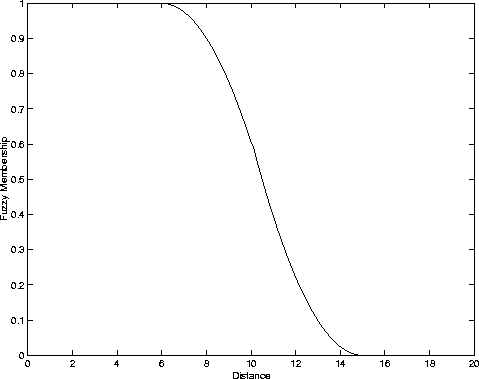
Figure 1
The same S' function can also be used for many other single valued criteria, such as a house that costs less than $300,000 etc.
If the fuzzy variables have multiple classes, then the above S' function cannot be used and we need a membership function that can assign partial memberships to the various classes. These memberships can be assigned in various ways and in this paper we explain two ways in which this can be accomplished.
2.1.2 The following method of evaluating the membership functions can be used when a variable is broadly classified to a few classes and there are sharp boundaries between the classes. For example, if the fuzzy variable is slope and if slope is classified as gentle, medium and steep, and if the areas with slope between 0\% and 20\% are defined as areas with gentle slope, then, a particular feature having a slope 19.9\% would be classified into the category `gentle' if a conventional box classification is used even though logically it is equally or even more likely to belong to the class `medium'. A classification of 19.95\% into the category `gentle' could lead to a wrong decision and consequently an inefficient planning. Such issues are solved by assigning partial memberships to the classes. A full membership is indicated by assigning 1 as the membership value and a lack of membership is indicated by assigning 0. A fuzzy set is, hence defined by assigning to each class a value which would represent its grade of membership in that particular class. This grade corresponds to the degree to which an individual is similar to the concept represented by the fuzzy set. Hence, the transition from one class to another is more gradual than abrupt.
Many times, a polygon based analysis is performed rather than a pixel-based analysis. In such cases, most of the time an average of all cell values is used as an estimate for the whole polygon. This introduces an uncertainity in the measurement of the variable. Using this uncertainty as the basis for deriving the Fuzzy membership functions, a Gaussian Error Function Membership Function as defined by Sasikala & Petrou [2] is used. Let us assume that the class membership of a fuzzy variable is determined by a measurement concerning the variable, performed with a given accuracy expressed by the standard error in the measuring process. In other words, let us say that the value of a given variable t is measured to be the mean and the error in this measurement is assumed to be Gaussianly distributed with zero mean and standard deviation sigma. Our objective is to derive the membership functions of classes defined for the variable t as ranges of its values. Using the probability density function of a Gaussian curve and using the definitions of error functions, we derived the following equation that gives the probability of the variable t belonging to a class c.
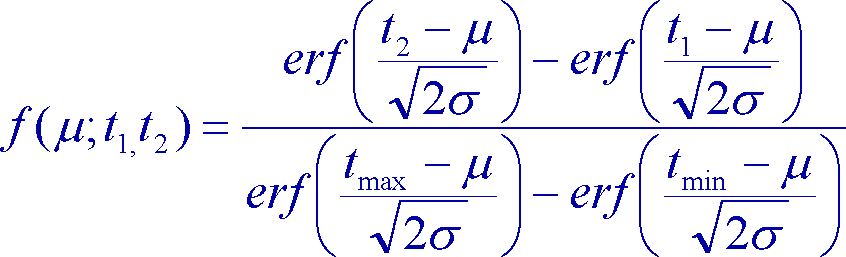
where
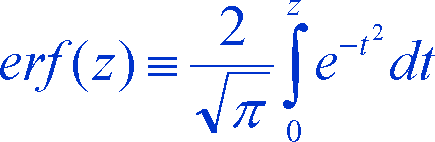
The memberships functions obtained using this equation is shown graphically below.
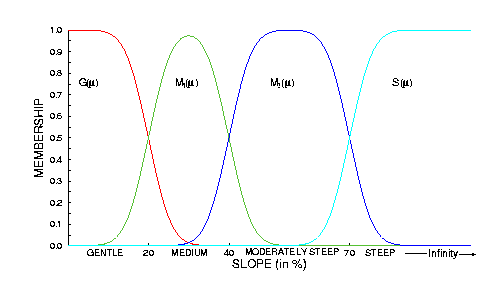
Figure 2
The detailed derivation can be found in earlier publications [1][2].
2.1.3 When there is a mixture of thematic classes within a region or polygon, the simplest way of assigning partial membership values to the classes would be by evaluating the proportion of cells or area belonging to a particular class of the variable and using that proportion as the fuzzy membership value.
There are no strict guidelines for choosing a fuzzy membership function. Hence, any function that satisfies a few basic conditions can be used.
2.2 Fuzzy Multi-Criteria Aggregation
Once the fuzzy membership values are obtained for each criterion, the next step would be to select features that satisfy all these criteria. Hence, we need to aggregate the various criteria by combining the fuzzy membership values of the various criteria. Consider the example given in Table 1.

Table 1
This table shows that Limitation to Natural Regeneration Potential of Soil is influenced by two criteria, namely Soil Depth and Aspect. It also gives the rules given by experts. For example, one of the rules states that, If Soil is Deep and Aspect is North then there is No Limitation (NL) to Regeneration Potential. By using the membership functions explained in Section 2.1.2, we would have fuzzy membership values into the various classes of Soil Depth and Aspect. Since each polygon would now have memberships in each class, we need a method of aggregating the multiple values of Soil Depth with those of Aspect. The evaluation of membership for No Limitation (NL) can be represented as follows.
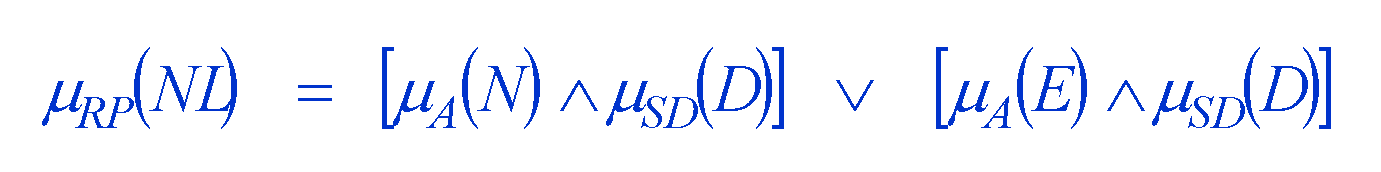
where V represents an OR operator and inverted V represents an AND operator. This aggregation can be achieved by using Fuzzy Aggregation operators. Most of the criteria are combined with either an AND or OR operator. There are many Fuzzy Aggregation operators that serve as AND and OR operators. Table 2 shows some of these operators.

Table 2
In the example stated on Limitation to Natural Regeneration Potential, these aggregation operators can be used to evaluate the membership values to the various classes of Limitation to Natural Regeneration Potential. A training process can also be used to choose the optimal operators. The relative importances can be either multiplied with the fuzzy membership values or raised to the power. The details of incorporating the weights can be found in [2].
3. ConclusionThis paper expained how a Multi-Criteria GIS Analysis can be performed using a Fuzzy Reasoning. An experiment was performed using these methods at the Center for Mapping, using Esri's MapObjects and Visual Basic. This experiment revealed the fact that implementing Fuzzy Reasoning in a Decision Support System is easy and also improves the accuracy of analysis to a great extent. More details of the Fuzzy methods in GIS can be found in [1]. [2][3][4] give the experiments performed using Fuzzy Reasoning in evaluating the Risk of Desertification of a forest affected by fire. No analysis can be efficient unless the cognitive uncertainties involved in the problem are handled and hence using Fuzzy reasoning in GIS analysis is indispensable.
References
1. Sasikala Ganesan, FuzzyGIS, submitted to International Journal of Geographical Information Science, in April 1999.
2. K. R. Sasikala and M. Petrou, Generalised Fuzzy Aggregation in Estimating the Risk of Desertification of a burned forest, accepted for publication in Fuzzy Sets and Systems.
3. K. R. Sasikala, M. Petrou, J. Kittler, Fuzzy Reasoning with a GIS for decision making in burnt-forest management, EARSeL Advances in Remote Sensing, Vol 44, No 4, Sep 1996.
4. K. R. Sasikala, M. Petrou, J. Kittler, Comparison of different Fuzzy Logic Rules for Uncertain Reasoning with a GIS in a series in Remote Sensing, Vol. 1, titled Soft Computing in Remote Sensing Data Analysis, World Scientific press, pp 121-128.